
| A. | 3600 | B. | 350 | C. | 4800 | D. | 480 |
分析 设本季度生产A家电x台、B家电y台,则生产家电C:120-x-y台,总产值为z千元,由题意列出关于x,y的不等式组,再求出线性目标函数z=20x+30y+40(120-x-y)=4800-20x-10,由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答  解:设本季度生产A家电x台、B家电y台,则生产家电C:120-x-y台,总产值为z千元,
解:设本季度生产A家电x台、B家电y台,则生产家电C:120-x-y台,总产值为z千元,
| 家电名称 | A | B | C |
| 工 时 | 3 | 4 | 6 |
| 产值(千元) | 20 | 30 | 40 |
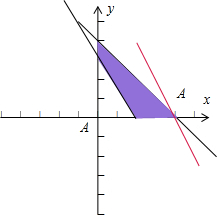
点评 本题考查简单的线性规划,考查了简单的数学建模思想方法,考查数形结合的解题思想方法,是中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
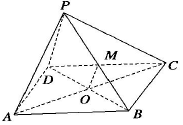 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 海军某舰队在一未知海域向正西方向行驶(如图),在A处测得北侧一岛屿的顶端D的底部C在西偏北30°的方向上,行驶4千米到达B处后,测得该岛屿的顶端D的底部C在西偏北75°方向上,山顶D的仰角为30°,求此岛屿露出海平面的部分CD的高度.
海军某舰队在一未知海域向正西方向行驶(如图),在A处测得北侧一岛屿的顶端D的底部C在西偏北30°的方向上,行驶4千米到达B处后,测得该岛屿的顶端D的底部C在西偏北75°方向上,山顶D的仰角为30°,求此岛屿露出海平面的部分CD的高度.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com