
【题目】设椭圆![]() ,定义椭圆
,定义椭圆![]() 的“相关圆”方程为
的“相关圆”方程为![]() .若抛物线
.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,且椭圆
的一个焦点重合,且椭圆![]() 短轴的一个端点和其两个焦点构成直角三角形.
短轴的一个端点和其两个焦点构成直角三角形.
(1)求椭圆![]() 的方程和“相关圆”
的方程和“相关圆”![]() 的方程;
的方程;
(2)过“相关圆”![]() 上任意一点
上任意一点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.![]() 为坐标原点,若
为坐标原点,若![]() ,证明原点
,证明原点![]() 到直线
到直线![]() 的距离是定值,并求
的距离是定值,并求![]() 的取值范围.
的取值范围.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
【题目】已知平面上动点P到定点![]() 的距离比P到直线
的距离比P到直线![]() 的距离大1.记动点P的轨迹为曲线C.
的距离大1.记动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点![]() 的直线
的直线![]() 交曲线C于A、B两点,点A关于x轴的对称点是D,证明:直线
交曲线C于A、B两点,点A关于x轴的对称点是D,证明:直线![]() 恒过点F.
恒过点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄金分割比例![]() 具有严格的比例性,艺术性,和谐性,蕴含着丰富的美学价值.这一比值能够引起人们的美感,被称为是建筑和艺术中最理想的比例.我们把离心率
具有严格的比例性,艺术性,和谐性,蕴含着丰富的美学价值.这一比值能够引起人们的美感,被称为是建筑和艺术中最理想的比例.我们把离心率![]() 的椭圆称为“黄金椭圆”,则以下四种说法中正确的个数为( )
的椭圆称为“黄金椭圆”,则以下四种说法中正确的个数为( )
①椭圆![]() 是“黄金椭圆;
是“黄金椭圆;
②若椭圆![]() ,
,![]() 的右焦点
的右焦点![]() 且满足
且满足![]() ,则该椭圆为“黄金椭圆”;
,则该椭圆为“黄金椭圆”;
③设椭圆![]() ,
,![]() 的左焦点为F,上顶点为B,右顶点为A,若
的左焦点为F,上顶点为B,右顶点为A,若![]() ,则该椭圆为“黄金椭圆”;
,则该椭圆为“黄金椭圆”;
④设椭圆,![]() ,
,![]() 的左右顶点分别A,B,左右焦点分别是
的左右顶点分别A,B,左右焦点分别是![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,则该椭圆为“黄金椭圆”;
成等比数列,则该椭圆为“黄金椭圆”;
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 表示从左到右依次排列的9盏灯,现制定开灯与关灯的规则如下:
表示从左到右依次排列的9盏灯,现制定开灯与关灯的规则如下:
(1)对一盏灯进行开灯或关灯一次叫做一次操作;
(2)灯![]() 在任何情况下都可以进行一次操作;对任意的
在任何情况下都可以进行一次操作;对任意的![]() ,要求灯
,要求灯![]() 的左边有且只有灯
的左边有且只有灯![]() 是开灯状态时才可以对灯
是开灯状态时才可以对灯![]() 进行一次操作.如果所有灯都处于开灯状态,那么要把灯
进行一次操作.如果所有灯都处于开灯状态,那么要把灯![]() 关闭最少需要_____次操作;如果除灯
关闭最少需要_____次操作;如果除灯![]() 外,其余8盏灯都处于开灯状态,那么要使所有灯都开着最少需要_____次操作.
外,其余8盏灯都处于开灯状态,那么要使所有灯都开着最少需要_____次操作.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)已知函数![]() ,其中正确结论的是( )
,其中正确结论的是( )
A.当![]() 时,函数
时,函数![]() 有最大值.
有最大值.
B.对于任意的![]() ,函数
,函数![]() 一定存在最小值.
一定存在最小值.
C.对于任意的![]() ,函数
,函数![]() 是
是![]() 上的增函数.
上的增函数.
D.对于任意的![]() ,都有函数
,都有函数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学专著《九章算术》中有一个“两鼠穿墙题”,其内容为:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半.问何日相逢?各穿几何?”如图的程序框图源于这个题目,执行该程序框图,若输入x=20,则输出的结果为( )
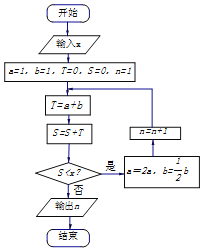
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() ,直线
,直线![]() 与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为
与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为![]() 。
。
(1)求椭圆E的方程;
(2)M为椭圆E在第一象限部分上一点,直线MP与椭圆交于另一点N,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为![]() 的正方形
的正方形![]() 沿对角线
沿对角线![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,在折起后形成的三棱锥
,在折起后形成的三棱锥![]() 中,给出下列四个命题:①
中,给出下列四个命题:①![]() ;②异面直线
;②异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;③二面角
;③二面角![]() 余弦值为
余弦值为![]() ;④三棱锥
;④三棱锥![]() 的体积是
的体积是![]() .其中正确命题的序号是___________.(写出所有正确命题的序号)
.其中正确命题的序号是___________.(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com