
【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
【答案】(1)![]() ;(2)分布列见解析.
;(2)分布列见解析.
【解析】
试题分析:(1)由题意知![]() 名志愿者每人任选一天参加社区服务,共有
名志愿者每人任选一天参加社区服务,共有![]() 种不同的结果,这些结果出现的可能性都相等.满足条件的事件是
种不同的结果,这些结果出现的可能性都相等.满足条件的事件是![]() 名志愿者恰好连续
名志愿者恰好连续![]() 天参加社区服务工作共包括
天参加社区服务工作共包括![]() 不同的结果.根据概率公式做出概率;(2)
不同的结果.根据概率公式做出概率;(2)![]() 表示这
表示这![]() 名志愿者在
名志愿者在![]() 月
月![]() 号参加社区服务工作的人数,随机变量
号参加社区服务工作的人数,随机变量![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,类似于第一问的做法,写出变量的分布列,得到要求的结果.
,类似于第一问的做法,写出变量的分布列,得到要求的结果.
试题解析:(1)![]() 名志愿者每人任选一天参加社区服务,共有
名志愿者每人任选一天参加社区服务,共有![]() 种不同的结果,这些结果出现的可能性都
种不同的结果,这些结果出现的可能性都
相等.设“![]() 名志愿者恰好连续
名志愿者恰好连续![]() 天参加社区服务工作”为事件
天参加社区服务工作”为事件![]() 则该事件共包括
则该事件共包括![]() 不同的结果.
不同的结果.
所以![]() ;
;
(2)![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
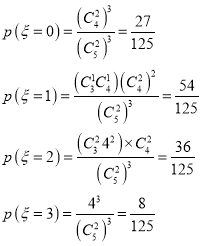
∴
| 0 | 1 | 2 | 3 | |||||
|
|
|
|
| |||||
|
|
|
|
| |||||
|
|
|
|
| |||||


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片。当初向各地作了广告推广,同时广告对销售收益也有影响。在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
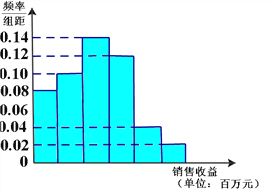
(Ⅰ)根据频率分布直方图,计算图中各小长方形的宽度;
(Ⅱ)根据频率分布直方图,估计投入4万元广告费用之后,并将各地销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:百万元) | 2 | 3 | 2 | 7 |
表中的数据显示,![]() 与
与![]() 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算![]() 关于
关于![]() 的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为
的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为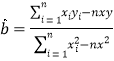 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)对于曲线上的不同两点![]() ,如果存在曲线上的点
,如果存在曲线上的点![]() ,且
,且![]() 使得曲线在点
使得曲线在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 为弦
为弦![]() 的伴随直线,特别地,当
的伴随直线,特别地,当![]() 时,又称
时,又称![]() 为
为![]() 的
的![]() —伴随直线.
—伴随直线.
①求证:曲线![]() 的任意一条弦均有伴随直线,并且伴随直线是唯一的;
的任意一条弦均有伴随直线,并且伴随直线是唯一的;
②是否存在曲线![]() ,使得曲线
,使得曲线![]() 的任意一条弦均有
的任意一条弦均有![]() —伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
—伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司拟投资开发某项新产品,市场评估能获得10~1 000万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不低于1万元,同时不超过投资收益的20%.
(1) 设奖励方案的函数模型为f(x),试用数学语言表述公司对奖励方案的函数模型f(x)的基本要求;
(2) 公司能不能用函数f(x)=![]() +2作为预设的奖励方案的模型函数?
+2作为预设的奖励方案的模型函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]()
![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图5所示:将
的一段图象如图5所示:将![]() 的图像向右平移
的图像向右平移![]() 个单位,可得到函数
个单位,可得到函数![]() 的图象,且图像关于原点对称,
的图象,且图像关于原点对称,

(1)求![]() 的值;
的值;
(2)求![]() 的最小值,并写出
的最小值,并写出![]() 的表达式;
的表达式;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上最小值为
上最小值为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com