
【题目】在投掷骰子试验中,根据向上的点数可以定义许多事件,如:A={出现1点},B={出现3点或4点},C={出现的点数是奇数},D={出现的点数是偶数}.
(1)说明以上4个事件的关系.
(2)求两两运算的结果.
【答案】(1)见解析;(2)见解析.
【解析】试题分析(1)已知事件![]() 的定义,首先由题意确定骰子向上可能出现的点数以及各个点数的出现能不能同时发生即可确定事件之间的关系;(2)根据互斥事件的加法概率公式对事件
的定义,首先由题意确定骰子向上可能出现的点数以及各个点数的出现能不能同时发生即可确定事件之间的关系;(2)根据互斥事件的加法概率公式对事件![]() 发生的概率进行计算,进而得出最终答案.
发生的概率进行计算,进而得出最终答案.
试题解析:在投掷骰子的试验中,根据向上出现的点数有6种基本事件,
记作Ai={出现的点数为i}(其中i=1,2,…,6).则A=A1,B=A3∪A4,
C=A1∪A3∪A5,D=A2∪A4∪A6.
(1)事件A与事件B互斥,但不对立,事件A包含于事件C,事件A与D互斥,但不对立;事件B与C不是互斥事件,事件B与D也不是互斥事件;事件C与D是互斥事件,也是对立事件.
(2)A∩B=![]() ,A∩C=A,A∩D=
,A∩C=A,A∩D=![]() .
.
A∪B=A1∪A3∪A4={出现的点数为1或3或4},
A∪C=C={出现的点数为1或3或5},
A∪D=A1∪A2∪A4∪A6={出现的点数为1或2或4或6}.
B∩C=A3={出现的点数为3},
B∩D=A4={出现的点数为4}.
B∪C= A1∪A3∪A4∪A5={出现的点数为1或3或4或5}.
B∪D=A2∪A3∪A4∪A6={出现的点数为2或3或4或6}.
C∩D=![]() ,C∪D=A1∪A2∪A3∪A4∪A5∪A6={出现的点数为1,2,3,4,5,6}.
,C∪D=A1∪A2∪A3∪A4∪A5∪A6={出现的点数为1,2,3,4,5,6}.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】当前,网购已成为现代大学生的时尚。某大学学生宿舍4人参加网购,约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有1人去淘宝网购物的概率;
(2)用![]() 分别表示这4个人中去淘宝网和京东商城购物的人数,记
分别表示这4个人中去淘宝网和京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() .若对任意的
.若对任意的![]() ,
, ![]() 都有
都有![]() .
.
(1)用函数单调性的定义证明: ![]() 在定义域上为增函数;
在定义域上为增函数;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有的
对所有的![]() 和
和![]() 都恒成立,求实数
都恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序的功能是( )
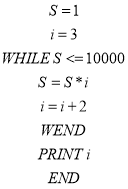
A. 求1×2×3×4×…×10 00的值
B. 求2×4×6×8×…×10 000的值
C. 求3×5×7×9×…×10 001的值
D. 求满足1×3×5×…×n>10 000的最小正整数n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com