
分析 (1)△ABC中,由$\overrightarrow{m}$⊥$\overrightarrow{n}$,可得$\overrightarrow{m}•\overrightarrow{n}$=0,化简求得cosC=$\frac{1}{2}$,从而求得C的值.
(2)由已知得c=(2R)sinC=2sin$\frac{π}{3}$=$\sqrt{3}$,由a2+b2≥2ab,即c2+ab≥2ab,得ab≤3.由此能求出△ABC面积的最大值.
解答 解:(1)△ABC中,∵$\overrightarrow{m}$⊥$\overrightarrow{n}$,可得$\overrightarrow{m}•\overrightarrow{n}$=0,
∴2sin2$\frac{A+B}{2}$+cos2C-1=0⇒cos2C+cosC=0,
∴2cos2C+cosC-1=0,
∴cosC=$\frac{1}{2}$,即C=$\frac{π}{3}$.
(2)∵△ABC的外接圆半径为R=1,∠C=$\frac{π}{3}$,
∴c=(2R)sinC=2sin$\frac{π}{3}$=$\sqrt{3}$,
∵a2+b2≥2ab,即c2+ab≥2ab,
∴ab≤c2,即ab≤3.
故S△ABC=$\frac{1}{2}$absin$\frac{π}{3}$≤$\frac{3}{2}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
∴△ABC面积的最大值为$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查两个向量垂直的性质,两个向量的数量积公式,余弦定理,根据三角函数的值求角,考查三角形面积的最大值的求法,解题时要认真审题,注意正弦定理的合理运用.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若直线l平行于平面α内的无数条直线,则l∥α | |
| B. | 若直线a在平面α外,则a∥α | |
| C. | 若直线a∥b,b?α,则a∥α | |
| D. | 若直线a∥b,b?α,则直线a就平行于平面内的无数条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
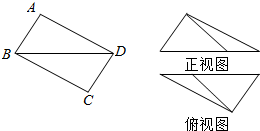 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{25}$ | D. | $\frac{36}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com