
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| (xn-1-yn-1)2+(xn-1+yn-1)2 |
| ||
| 2 |
| xn-12+yn-12 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| an-1•an |
| |an-1|•|an| |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
| a |
| a |
| a |
| 1 |
| 2 |
| a |
| a |
| a |
| 1 |
| 2 |
| a |
| a |
| a |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:江西省红色六校2012届高三第二次联考数学文科试题 题型:022
已知一非零向量数列{![]() }满足
}满足![]() =(1,1)
=(1,1)![]() =(xn,yn)=
=(xn,yn)=![]() (xn-1-yn-1,xn-1+yn-1)(n≥2且n∈N*).给出以下结论:
(xn-1-yn-1,xn-1+yn-1)(n≥2且n∈N*).给出以下结论:
①数列{|![]() |}是等差数列,②
|}是等差数列,②![]() ;③设cn=2log2|
;③设cn=2log2|![]() |,则数列{cn}的前n项和为Tn,当且仅当n=2时,Tn取得最大值;④记向量
|,则数列{cn}的前n项和为Tn,当且仅当n=2时,Tn取得最大值;④记向量![]() 与
与![]() 的夹角为
的夹角为![]() n(n≥2),均有
n(n≥2),均有![]() n=
n=![]() .其中所有正确结论的序号是________
.其中所有正确结论的序号是________
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省红色六校高三第二次联考文科数学试卷 题型:填空题
已知一非零向量数列 满足
满足

 。给出以下结论:
。给出以下结论:
1.数列 是等差数列,2。
是等差数列,2。 ;3。设
;3。设 ,则数列
,则数列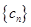 的前n项和为
的前n项和为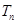 ,当且仅当n=2时,
,当且仅当n=2时,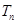 取得最大值;4。记向量
取得最大值;4。记向量 与
与 的夹角为
的夹角为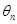 (
( ),均有
),均有 。其中所有正确结论的序号是____
。其中所有正确结论的序号是____
查看答案和解析>>
科目:高中数学 来源:江西省红色六校2011-2012学年高三第二次联考数学(文)试题 题型:填空题
已知一非零向量数列 满足
满足

 。给出以下结论:
。给出以下结论:
①数列 是等差数列,②
是等差数列,② ;③设
;③设 ,则数列
,则数列 的前n项和为
的前n项和为 ,当且仅当n=2时,
,当且仅当n=2时, 取得最大值;④记向量
取得最大值;④记向量 与
与 的夹角为
的夹角为 (
( ),均有
),均有 。其中所有正确结论的序号是_____________
。其中所有正确结论的序号是_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com