
分析 (1)当直线l与x轴垂直时,由sAMBN=$\frac{1}{2}•2a•\frac{2{b}^{2}}{a}=2$,得b.
又|$\overrightarrow{M{F}_{2}}$|=$\sqrt{2}$|$\overrightarrow{AB}$|+|$\overrightarrow{{F}_{2}N}$|,所以a+c=$\sqrt{2}•\frac{2{b}^{2}}{a}+a-c$,即ac=$\sqrt{2}$,又a2=c2+1,解得a即可.
(2)设A,(x1,y1),B(x2,y2),而M(-$\sqrt{2}$,0),N($\sqrt{2}$,0)
所以$\overrightarrow{AM}=(-\sqrt{2}-{x}_{1},-{y}_{1})$,$\overrightarrow{AN}=(\sqrt{2}-{x}_{1},-{y}_{1})$,$\overrightarrow{BM}=(-\sqrt{2}-{x}_{2},-{y}_{2})$,$\overrightarrow{BN}=(\sqrt{2}-{x}_{2},-{y}_{2})$.从而有$\overrightarrow{AM}•\overrightarrow{AN}+\overrightarrow{BM}•\overrightarrow{BN}$=$(-\sqrt{2}-{x}_{1})(\sqrt{2}-{x}_{1})+(-\sqrt{2}-{x}_{2})(\sqrt{2}-{x}_{2})$+${{y}_{1}}^{2}+{{y}_{2}}^{2}$=${{x}_{1}}^{2}+{{x}_{2}}^{2}+{{y}_{1}}^{2}+{{y}_{2}}^{2}-4$=(x1+x2)2-2x1x2+(y1+y2)2-2y1y2-4.再利用韦达定理及函数的值域即可.
解答 解:(1)当直线l与x轴垂直时,由sAMBN=$\frac{1}{2}•2a•\frac{2{b}^{2}}{a}=2$,得b=1.
又|$\overrightarrow{M{F}_{2}}$|=$\sqrt{2}$|$\overrightarrow{AB}$|+|$\overrightarrow{{F}_{2}N}$|,所以a+c=$\sqrt{2}•\frac{2{b}^{2}}{a}+a-c$,即ac=$\sqrt{2}$,又a2=c2+1,
解得a=$\sqrt{2}$.因此该椭圆的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)设A,(x1,y1),B(x2,y2),而M(-$\sqrt{2}$,0),N($\sqrt{2}$,0)
所以$\overrightarrow{AM}=(-\sqrt{2}-{x}_{1},-{y}_{1})$,$\overrightarrow{AN}=(\sqrt{2}-{x}_{1},-{y}_{1})$,
$\overrightarrow{BM}=(-\sqrt{2}-{x}_{2},-{y}_{2})$,$\overrightarrow{BN}=(\sqrt{2}-{x}_{2},-{y}_{2})$.
从而有$\overrightarrow{AM}•\overrightarrow{AN}+\overrightarrow{BM}•\overrightarrow{BN}$=$(-\sqrt{2}-{x}_{1})(\sqrt{2}-{x}_{1})+(-\sqrt{2}-{x}_{2})(\sqrt{2}-{x}_{2})$+${{y}_{1}}^{2}+{{y}_{2}}^{2}$
=${{x}_{1}}^{2}+{{x}_{2}}^{2}+{{y}_{1}}^{2}+{{y}_{2}}^{2}-4$=(x1+x2)2-2x1x2+(y1+y2)2-2y1y2-4.
因为直线l过椭圆的焦点(1,0),所以可以设直线l的方程为x=ty+1 (t∈R),则
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{x=ty+1}\end{array}\right.$消去x并整理,得(t2+2)y2+2ty-1=0,
所以y1+y2=$\frac{-2t}{{t}^{2}+2}$,y1y2=$\frac{-1}{{t}^{2}+2}$.
进而x1+x2=t(y1+y2)+2=$\frac{4}{{t}^{2}+2}$,x1x2=(ty1+1)(ty2+1)=$\frac{2-2{t}^{2}}{{t}^{2}+2}$,
可得有$\overrightarrow{AM}•\overrightarrow{AN}+\overrightarrow{BM}•\overrightarrow{BN}$=$\frac{8}{({t}^{2}+2)^{2}}-\frac{6}{{t}^{2}+2}$
令t2+2=m,则m≥2.从而有$\overrightarrow{AM}•\overrightarrow{AN}+\overrightarrow{BM}•\overrightarrow{BN}$=$\frac{8}{{m}^{2}}-\frac{6}{m}=8(\frac{1}{m}-\frac{3}{8})^{2}-\frac{9}{8}$,
而0<$\frac{1}{m}≤\frac{1}{2}$,所以求得$\overrightarrow{AM}•\overrightarrow{AN}+\overrightarrow{BM}•\overrightarrow{BN}$的取值范围是[-$\frac{9}{8}$,0].
点评 本题考查了直线与椭圆的位置关系,韦达定理,向量运算等运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{65}$ | B. | -$\frac{63}{65}$ | C. | -$\frac{33}{65}$ | D. | $\frac{63}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
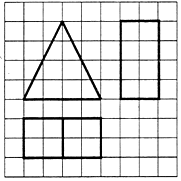
| A. | 16 | B. | $24+8\sqrt{5}$ | C. | 48 | D. | $24+16\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com