
分析 (Ⅰ)根据向量的数量积和向量的模,先求出$\overrightarrow{b}$,再根据向量的垂直即可求出x的值,
(Ⅱ)根据二次函数的性质即可求出x的值,再根据向量的夹角公式即可求出.
解答 解:(Ⅰ)设$\overrightarrow{b}$=(m,n),
∴$\left\{\begin{array}{l}{{m}^{2}+{n}^{2}=5}\\{3m-n=-5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=2}\end{array}\right.$或$\left\{\begin{array}{l}{m=-2}\\{n=-1}\end{array}\right.$,
当$\overrightarrow{b}$=(-1,2)时,
∴$\overrightarrow{c}$=x(3,-1)+(1-x)(-1,2)=(4x-1,2-3x),
∵$\overrightarrow{a}$$⊥\overrightarrow{c}$,
∴3(4x-1)-(2-3x)=0,
解得x=$\frac{1}{3}$,
当$\overrightarrow{b}$=(-2,-1)时,
∴$\overrightarrow{c}$=x(3,-1)+(1-x)(-2,-1)=(5x-2,-1),
∵$\overrightarrow{a}$$⊥\overrightarrow{c}$,
∴3(5x-2)+1=0,
解得x=$\frac{1}{3}$,
(Ⅱ)设$\overrightarrow{b}$与$\overrightarrow{c}$的夹角θ
由(Ⅰ)可知,当$\overrightarrow{b}$=(-1,2)时,$\overrightarrow{c}$=(4x-1,2-3x),
则|$\overrightarrow{c}$|2=(4x-1)2+(2-3x)2=25x2-20x+5=25(x-$\frac{2}{5}$)2+1,
当x=$\frac{2}{5}$时,|$\overrightarrow{c}$|取最小值,则|$\overrightarrow{c}$|=1,$\overrightarrow{c}$=($\frac{3}{5}$,$\frac{4}{5}$),
∴$\overrightarrow{b}•\overrightarrow{c}$=-$\frac{3}{5}$+$\frac{8}{5}$=1,|$\overrightarrow{b}$|=$\sqrt{5}$
∴cosθ=$\frac{\overrightarrow{b}•\overrightarrow{c}}{|\overrightarrow{b}|•|\overrightarrow{c}|}$=$\frac{\sqrt{5}}{5}$
当$\overrightarrow{b}$=(-2,-1)时,$\overrightarrow{c}$=(5x-2,-1),
则|$\overrightarrow{c}$|2=(5x-2)2+(-1)2=25(x-$\frac{2}{5}$)2+1,
当x=$\frac{2}{5}$时,|$\overrightarrow{c}$|取最小值,则|$\overrightarrow{c}$|=1,$\overrightarrow{c}$=(0,-1),
∴$\overrightarrow{b}•\overrightarrow{c}$=1,|$\overrightarrow{b}$|=$\sqrt{5}$
∴cosθ=$\frac{\overrightarrow{b}•\overrightarrow{c}}{|\overrightarrow{b}|•|\overrightarrow{c}|}$=$\frac{\sqrt{5}}{5}$
点评 本题考查了向量的数量积的运算和向量的垂直以及二次函数的性质,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
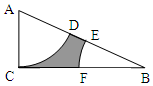 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .16或36 | B. | 36或64 | C. | 16或64 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
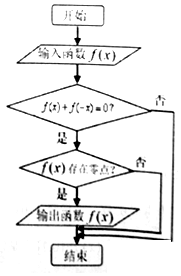 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x4 | C. | f(x)=2x | D. | f(x)=x-$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com