

 化成
化成
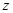 变化时,它表示一组平行直线,当该直线经过可行域且在
变化时,它表示一组平行直线,当该直线经过可行域且在 轴上的截距最大时
轴上的截距最大时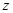 最大.依此找出最优解,求得
最大.依此找出最优解,求得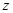 的最大值.
的最大值.

 :2x+3y=0向右上方平移至
:2x+3y=0向右上方平移至 的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值
的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值 得M的坐标为(2,3)
得M的坐标为(2,3) 千元
千元

 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源:不详 题型:单选题
A.y=x+
| ||||||
B.y=
| ||||||
C.y=
| ||||||
D.y=2-3x-
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为( )
,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为( )| A.45 | B.36 | C.30 | D.27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com