
【题目】用![]() 表示自然数n的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
表示自然数n的所有因数中最大的那个奇数,例如:9的因数有1,3,9,![]() ,10的因数有1,2,5,10,
,10的因数有1,2,5,10,![]() ,那么
,那么![]() ______.
______.
【答案】![]()
【解析】
根据题中对g(n)的定义,判断出g(n)=g(2n),且若n为奇数则g(n)=n,利用等差数列的前n项和公式及逐差累加的方法及等比数列的前n项和公式求出g(1)+g(2)+g(3)+…+g(2n﹣1),令n=22018﹣1求出g(1)+g(2)+g(3)+…+g(22018﹣1).
由g(n)的定义易知g(n)=g(2n),且若n为奇数则g(n)=n,
令f(n)=g(1)+g(2)+g(3)+…g(2n﹣1),
则f(n+1)=g(1)+g(2)+g(3)+…g(2n+1﹣1)=1+3+…+(2n+1﹣1)+g(2)+g(4)+…+g(2n+1﹣2)
![]() g(1)+g(2)+…+g(2n+1﹣2)=4n+f(n),
g(1)+g(2)+…+g(2n+1﹣2)=4n+f(n),
即f(n+1)﹣f(n)=4n,
分别取n为1,2,…,n并累加得f(n+1)﹣f(1)=4+42+…+4n![]() (4n﹣1),
(4n﹣1),
又f(1)=g(1)=1,所以f(n+1)![]() (4n﹣1)+1,
(4n﹣1)+1,
所以f(n)=g(1)+g(2)+g(3)+…g(2n﹣1)![]() (4n﹣1﹣1)+1,
(4n﹣1﹣1)+1,
令n=22018﹣1,得:
g(1)+g(2)+g(3)+…+g(22018﹣1)![]() (42018﹣1﹣1)+1
(42018﹣1﹣1)+1![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:

(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品![]() 和
和![]() ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
投资结果 | 获利20% | 获利10% | 不赔不赚 | 亏损10% |
概率 | 0.2 | 0.3 | 0.2 | 0.3 |
产品![]() (其中
(其中![]() )
)
投资结果 | 获利30% | 不赔不赚 | 亏损20% |
概率 |
| 0.1 |
|
(1)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求
进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求![]() 的取值范围;
的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪种产品?
之中选其一,应选用哪种产品?
查看答案和解析>>
科目:高中数学 来源: 题型:
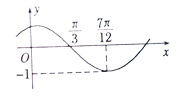
【题目】函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
)的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
A. 向右平移![]() 个单位长度 B. 向左平移
个单位长度 B. 向左平移![]() 个单位长度
个单位长度
C. 向右平移![]() 个单位长度 D. 向左平移
个单位长度 D. 向左平移![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区上年度电价为0.8元![]() ,年用电量为
,年用电量为![]() ,本年度计划将电价降到0.55 元
,本年度计划将电价降到0.55 元![]() 至0.75元
至0.75元![]() 之间,而用户期待电价为0.4元
之间,而用户期待电价为0.4元![]() ,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元
,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元![]() .(注:收益=实际用电量
.(注:收益=实际用电量![]() (实际电价-成本价)),示例:若实际电价为0.6元
(实际电价-成本价)),示例:若实际电价为0.6元![]() ,则下调电价后新增加的用电量为
,则下调电价后新增加的用电量为![]() 元
元![]() )
)
(1)写出本年度电价下调后,电力部门的收益![]() 与实际电价
与实际电价![]() 的函数关系;
的函数关系;
(2)设![]() ,当电价最低为多少仍可保证电力部门的收益比上一年至少增长
,当电价最低为多少仍可保证电力部门的收益比上一年至少增长![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,在某次考试成绩统计中,某老师为了对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差 | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)若![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该次考试该数平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据: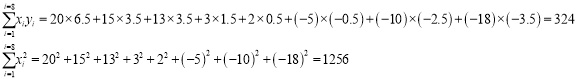
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

表1:设备改造后样本的频数分布表

(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;

(2)根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价240元;质量指标值落在
内的定为一等品,每件售价240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com