
【题目】如图所示,直角梯形公园![]() 中,
中,![]() ,
,![]() ,
,![]() ,公园的左下角阴影部分为以
,公园的左下角阴影部分为以![]() 为圆心,半径为
为圆心,半径为![]() 的
的![]() 圆面的人工湖,现设计修建一条与圆相切的观光道路
圆面的人工湖,现设计修建一条与圆相切的观光道路![]() (点
(点![]() 分别在
分别在![]() 与
与![]() 上),
上),![]() 为切点,设
为切点,设![]() .
.

(1)试求观光道路![]() 长度的最大值;
长度的最大值;
(2)公园计划在道路![]() 的右侧种植草坪,试求草坪
的右侧种植草坪,试求草坪![]() 的面积最大值.
的面积最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数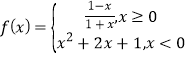 ,函数g(x)=f(1-x)-kx+k-
,函数g(x)=f(1-x)-kx+k-![]() 恰有三个不同的零点,则k的取值范围是( )
恰有三个不同的零点,则k的取值范围是( )
A. (-2-![]() ,0]∪
,0]∪![]() B. (-2+
B. (-2+![]() ,0]∪
,0]∪![]()
C. (-2-![]() ,0]∪
,0]∪![]() D. (-2+
D. (-2+![]() ,0]∪
,0]∪![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
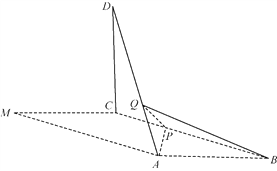
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为折痕将△
为折痕将△![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,
上一点,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是![]() 的导函数
的导函数![]() 的图象,对于下列四个判断,其中正确的判断是( ).
的图象,对于下列四个判断,其中正确的判断是( ).
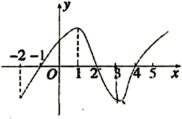
A.![]() 在
在![]() 上是增函数;
上是增函数;
B.当![]() 时,
时,![]() 取得极小值;
取得极小值;
C.![]() 在
在![]() 上是增函数、在
上是增函数、在![]() 上是减函数;
上是减函数;
D.当![]() 时,
时,![]() 取得极大值.
取得极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx3+x﹣sinx(m∈R).
(1)当m=0时,(i)求y=f(x)在(![]() ,f(
,f(![]() ))处的切线方程;
))处的切线方程;
(ii)证明:f(x)<ex;
(2)当x≥0时,函数f(x)单调递减,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com