
 如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.
如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.分析 ( I)由条件证明ED⊥BD,再根据BD⊥CD,利用直线和平面垂直的判定定理证得BD⊥平面ECD.
( II)先求△CBE的面积,Rt△BCD的面积,设点D到到面CEB的距离为h,利用等体积法求点D到平面CBE的距离h的值.
解答 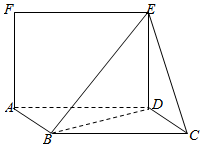 ( I)证明:∵四边形ADEF为正方形,
( I)证明:∵四边形ADEF为正方形,
∴ED⊥AD,
又∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
∴ED⊥平面ABCD,∴ED⊥BD.
又∵BD⊥CD,ED∩CD=D,
∴BD⊥平面ECD.
( II)解:∵CD=1,∠BCD=60°,BD⊥CD,
又∵正方形ADEF,∴CB=2,CE=$\sqrt{5}$,$BE=\sqrt{7}$,
∴$cos∠BCE=\frac{4+5-7}{{2×2×\sqrt{5}}}=\frac{{\sqrt{5}}}{10}$,∴${S_{△CEB}}=\frac{1}{2}×2×\sqrt{5}×\frac{{\sqrt{95}}}{10}=\frac{{\sqrt{19}}}{2}$,
Rt△BCD的面积等于 S△BCD=$\frac{1}{2}$•1•$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
由得( I)ED⊥平面ABCD,∴点E到平面BCD的距离为ED=2,设点D到到面CEB的距离为h,
∴${V_{D-CEB}}={V_{E-CDB}}=\frac{1}{3}.\frac{1}{2}.1.\sqrt{3}.2=\frac{{\sqrt{3}}}{3}$=$\frac{1}{3}×\frac{{\sqrt{19}}}{2}×h$,∴h=$\frac{2\sqrt{57}}{19}$,
即点D到到面CEB的距离为$\frac{2\sqrt{57}}{19}$.
点评 本题主要考查直线和平面垂直的判定和性质,利用等体积法求点到平面的距离,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,AD平分∠BAC交BC于D,交△ABC的外接圆于E.
如图,⊙O是△ABC的外接圆,AD平分∠BAC交BC于D,交△ABC的外接圆于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 大于40岁 | 16 | ||
| 小于或等于40岁 | 12 | ||
| 合计 | 80 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com