
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
试题第一问根据题意将问题转化为![]() 在区间
在区间![]() 上的最大值小于等于
上的最大值小于等于![]() 在区间
在区间![]() 上的最大值,之后根据函数的单调性求得相应的最值,第二问转化不等式,将问题转化为一个函数的最小值大于另一个函数的最大值,从而求得结果.
上的最大值,之后根据函数的单调性求得相应的最值,第二问转化不等式,将问题转化为一个函数的最小值大于另一个函数的最大值,从而求得结果.
试题解析:(Ⅰ) 由题意,![]() ,使得不等式
,使得不等式![]() 成立,
成立,
等价于![]() .1分
.1分
![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 时,
时,![]() 取得最大值1.即
取得最大值1.即![]()
又当![]() 时,
时,![]() ,
,![]()
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
故![]() 在区间
在区间![]() 上单调递减,因此,
上单调递减,因此,![]() 时,
时,![]() .
.
所以![]() ,则
,则![]() .
.
实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)当![]() 时,要证
时,要证![]() ,只要证
,只要证![]() ,
,
即证![]() ,由于
,由于![]() ,
,
只要证![]() .
.
下面证明![]() 时,不等式
时,不等式![]() 成立.
成立.
令![]() ,则
,则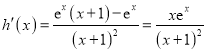 ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以当且仅当![]() 时,
时,![]() 取最小值为1.
取最小值为1.
法一:![]() ,则
,则![]() ,即
,即![]() ,即
,即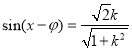 ,
,
由三角函数的有界性,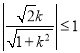 ,即
,即![]() ,所以
,所以![]() ,而
,而![]() ,
,
但当![]() 时,
时,![]() ;
;![]() 时,
时,![]()
所以,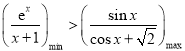 ,即
,即![]()
综上所述,当![]() 时,
时,![]() 成立.
成立.
法二:令![]() ,其可看作点
,其可看作点![]() 与点
与点![]() 连线的斜率
连线的斜率![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以直线
上,所以直线![]() 与圆
与圆![]() 相交或相切,
相交或相切,
当直线![]() 与圆
与圆![]() 相切且切点在第二象限时,
相切且切点在第二象限时,
直线![]() 取得斜率
取得斜率![]() 的最大值为
的最大值为![]() .而当
.而当![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .所以,
.所以,![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() 成立.
成立.
法三:令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 取得最大值1,而
取得最大值1,而![]() ,
,
但当![]() 时,
时,![]() ;
;![]() 时,
时,![]()
所以,![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() 成立.
成立.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】为增进市民的环保意识,某市有关部门面向全体市民进行了一次环保知识的微信问卷测试活动,每位市民仅有一次参与问卷测试机会.通过抽样,得到参与问卷测试的1000人的得分数据,制成频率分布直方图如图所示.

(1)估计成绩得分落在[86,100]中的概率.
(2)设这1000人得分的样本平均值为![]() .
.
(i)求![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(ii)有关部门为参与此次活动的市民赠送20元或10元的随机话费,每次获赠20元或10元的随机话费的概率分别为![]() 和
和![]() .得分不低于
.得分不低于![]() 的可获赠2次随机话费,得分低于
的可获赠2次随机话费,得分低于![]() 的可获赠1次随机话费.求一位市民参与这次活动获赠话费
的可获赠1次随机话费.求一位市民参与这次活动获赠话费![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)求直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 相交于点
相交于点![]() ,
,![]() ,设相交弦的长度为
,设相交弦的长度为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数且
为参数且![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
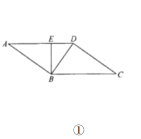
【题目】如图①:在平行四边形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起,使
折起,使![]() ,连结
,连结![]() ,得到如图②所示三棱锥
,得到如图②所示三棱锥![]() .
.
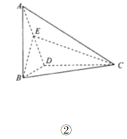
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,卷一《方田》中有如下两个问题:
[三三]今有宛田,下周三十步,径十六步.问为田几何?
[三四]又有宛田,下周九十九步,径五十一步.问为田几何?
翻译为:[三三]现有扇形田,弧长30步,直径长16步.问这块田面积是多少?
[三四]又有一扇形田,弧长99步,直径长51步.问这块田面积是多少?
则下列说法正确的是( )
A.问题[三三]中扇形的面积为240平方步B.问题[三四]中扇形的面积为![]() 平方步
平方步
C.问题[三三]中扇形的面积为60平方步D.问题[三四]中扇形的面积为![]() 平方步
平方步
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com