
【题目】已知函数f(x)=( ![]() )x﹣log2x,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:
)x﹣log2x,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:
①d>a;②d>b;③d<c;④d>c.其中可能成立的是(填序号)
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
, ![]() 为抛物线
为抛物线![]() :
: ![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中![]() 是0
是0![]() 9的某个整数)
9的某个整数)
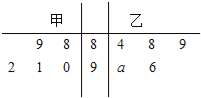
(1)若该厂决定从甲乙两人中选派一人去参加技能培训,从成绩稳定性角度考虑,你认为谁去比较合适?
(2)若从甲的成绩中任取两次成绩作进一步分析,在抽取的两次成绩中,求至少有一次成绩在(90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+bx+c,若f(﹣3)=f(1),f(0)=﹣3.
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() 画出函数g(x)图象;
画出函数g(x)图象;
(3)求函数g(x)在[﹣3,1]的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点![]() ,
,![]() ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为![]() ,直线
,直线![]() 与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为
与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,
(1)求实数a的取值范围,使函数y=f(x)在区间[﹣5,5]上是单调函数;
(2)若x∈[﹣5,5],记y=f(x)的最大值为g(a),求g(a)的表达式并判断其奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
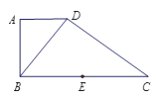
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() , 得到如
, 得到如
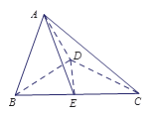
图所示的空间几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com