
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 上一点,以点
上一点,以点![]() 及椭圆的左、右焦点
及椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形面积为
为顶点的三角形面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作斜率存在且互相垂直的直线
作斜率存在且互相垂直的直线![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 两交点的中点,
两交点的中点,![]() 是
是![]() 与
与![]() 两交点的中点,求△
两交点的中点,求△![]() 面积的最大值.
面积的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
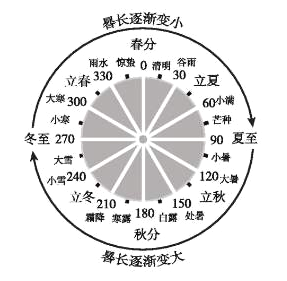
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立冬的晷长为一丈五寸
D.立春的晷长比立秋的晷长短
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是各项都为整数的等差数列,其前n项和为![]() ,
,![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设cn=log2b1+log2b2+log2b3+…+log2bn, ![]() .
.
(i)求Tn;
(ii)求证: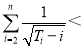 2.
2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程:
的参数方程: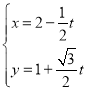 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com