
”¾ĢāÄæ”æijČĖÓŠĀ„·æŅ»“±£¬ŹŅÄŚĆ껿¹²¼Ę180m2 £¬ Äā·Öøī³ÉĮ½Ąą·æ¼ä×÷ĪŖĀĆÓĪæĶ·æ£¬“ó·æ¼äĆæ¼äĆ껿ĪŖ18m2 £¬ æÉ×”ÓĪæĶ5Ćū£¬ĆæĆūÓĪæĶĆæĢģ×”ĖŽ·Ń40ŌŖ£»Š”·æ¼äĆæ¼äĆ껿ĪŖ15m2 £¬ æÉŅŌ×”ÓĪæĶ3Ćū£¬ĆæĆūÓĪæĶĆæĢģ×”ĖŽ·Ń50ŌŖ£»×°ŠŽ“ó·æ¼äĆæ¼äŠčŅŖ1000ŌŖ£¬×°ŠŽŠ”·æ¼äĆæ¼äŠčŅŖ600ŌŖ£®Čē¹ūĖūÖ»Äܳļæī8000ŌŖÓĆӌװŠŽ£¬ĒŅ¼Ł¶ØÓĪæĶÄÜ×”ĀśæĶ·æ£¬ĖūÓ¦øō³ö“ó·æ¼äŗĶŠ”·æ¼äø÷¶ąÉŁ¼ä£¬²ÅÄÜ»ńµĆ×ī“óŹÕŅę£æ 
”¾“š°ø”æ½ā£ŗÉč·Öøī“ó·æ¼äĪŖx¼ä£¬Š”·æ¼äĪŖy¼ä£¬ŹÕŅęĪŖzŌŖ
øł¾ŻĢāŅāµĆ£ŗ 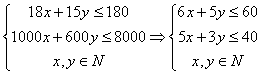
Ēó£ŗz=200x+150yµÄ×ī“óÖµ£®
×÷³öŌ¼ŹųĢõ¼ž±ķŹ¾µÄĘ½ĆęĒųÓņ
°ŃÄæ±źŗÆŹżz=200x+150y»ÆĪŖ ![]()
Ę½ŅĘÖ±Ļߣ¬Ö±ĻßŌ½ĶłÉĻŅĘ£¬zŌ½“ó£¬
ĖłŅŌµ±Ö±Ļß¾¹żMµćŹ±£¬zµÄÖµ×ī“ó£¬
½ā·½³Ģ×é ![]() µĆ
µĆ ![]() £¬
£¬
ŅņĪŖ×īÓŽāÓ¦øĆŹĒÕūŹż½ā£¬Ķعżµ÷ÕūµĆ£¬µ±Ö±Ļß¹żM'£Ø3£¬8£©ŗĶM'£Ø0£¬12£©Ź±z×ī“ó
ĖłŅŌµ±“ó·æ¼äĪŖ3¼ä£¬Š”·æ¼äĪŖ8¼ä»ņ“ó·æ¼äĪŖ0¼ä£¬Š”·æ¼äĪŖ12¼äŹ±£¬æÉ»ń×ī“óµÄŹÕŅęĪŖ1800ŌŖ£®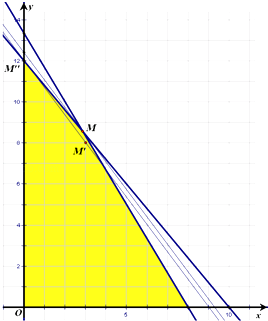
”¾½āĪö”æĻČÉč·Öøī“ó·æ¼äĪŖx¼ä£¬Š”·æ¼äĪŖy¼ä£¬ŹÕŅęĪŖzŌŖ£¬ĮŠ³öŌ¼ŹųĢõ¼ž£¬ŌŁøł¾ŻŌ¼ŹųĢõ¼ž»³öæÉŠŠÓņ£¬Éčz=200x+150y£¬ŌŁĄūÓĆzµÄ¼øŗĪŅāŅåĒó×īÖµ£¬Ö»ŠčĒó³öÖ±Ļßz=200x+150y¹żæÉŠŠÓņÄŚµÄÕūŹżµćŹ±£¬“Ó¶ųµĆµ½zÖµ¼“æÉ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £¬ĘäÖŠŹµŹż
£¬ĘäÖŠŹµŹż![]() ĪŖ³£Źż£¬
ĪŖ³£Źż£¬![]() ĪŖ×ŌČ»¶ŌŹżµÄµ×Źż.
ĪŖ×ŌČ»¶ŌŹżµÄµ×Źż.
£Ø1£©µ±![]() Ź±£¬ĒóŗÆŹż
Ź±£¬ĒóŗÆŹż![]() µÄµ„µ÷Ēų¼ä£»
µÄµ„µ÷Ēų¼ä£»
£Ø2£©µ±![]() Ź±£¬½ā¹ŲÓŚ
Ź±£¬½ā¹ŲÓŚ![]() µÄ²»µČŹ½
µÄ²»µČŹ½![]() £»
£»
£Ø3£©µ±![]() Ź±£¬Čē¹ūŗÆŹż
Ź±£¬Čē¹ūŗÆŹż![]() ²»“ęŌŚ¼«Öµµć£¬Ēó
²»“ęŌŚ¼«Öµµć£¬Ēó![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹żŌµćµÄ¶ÆÖ±ĻßlÓėŌ²C1£ŗx2+y2©6x+5=0Ļą½»ÓŚ²»Ķ¬µÄĮ½µćA£¬B£®
£Ø1£©ĒóŌ²C1µÄŌ²ŠÄ×ų±ź£»
£Ø2£©ĒóĻ߶ĪAB µÄÖŠµćMµÄ¹ģ¼£CµÄ·½³Ģ£»
£Ø3£©ŹĒ·ń“ęŌŚŹµŹż k£¬Ź¹µĆÖ±ĻßL£ŗy=k£Øx©4£©ÓėĒśĻß CÖ»ÓŠŅ»øö½»µć£æČō“ęŌŚ£¬Ēó³ökµÄȔֵ·¶Ī§£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“Óij¾ÓĆńĒųĖ껜³éČ”10øö¼ŅĶ„£¬»ńµĆµŚiøö¼ŅĶ„µÄŌĀŹÕČėxi£Øµ„Ī»£ŗĒ§ŌŖ£©ÓėŌĀ“¢Šīyi£Øµ„Ī»£ŗĒ§ŌŖ£©µÄŹż¾Ż×ŹĮĻ£¬ĖćµĆ ![]() £¬
£¬ ![]() £¬
£¬ ![]() £¬
£¬ ![]() £®
£®
£Ø¢ń£©Ēó¼ŅĶ„µÄŌĀ“¢Šīy¶ŌŌĀŹÕČėxµÄĻߊŌ»Ų¹é·½³Ģy=bx+a£»
£Ø¢ņ£©ÅŠ¶Ļ±äĮæxÓėyÖ®¼äŹĒÕżĻą¹Ų»¹ŹĒøŗĻą¹Ų£»
£Ø¢ó£©ČōøĆ¾ÓĆńĒųij¼ŅĶ„ŌĀŹÕČėĪŖ7Ē§ŌŖ£¬Ō¤²āøĆ¼ŅĶ„µÄŌĀ“¢Šī£®
ø½£ŗĻߊŌ»Ų¹é·½³Ģy=bx+aÖŠ£¬ 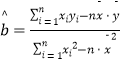 £¬
£¬ ![]() £¬ĘäÖŠ
£¬ĘäÖŠ ![]() £¬
£¬ ![]() ĪŖŃł±¾Ę½¾łÖµ£¬ĻߊŌ»Ų¹é·½³ĢŅ²æÉŠ“ĪŖ
ĪŖŃł±¾Ę½¾łÖµ£¬ĻߊŌ»Ų¹é·½³ĢŅ²æÉŠ“ĪŖ ![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčaŹĒŹµŹż£¬f£Øx£©=a© ![]() £Øx”ŹR£©£®
£Øx”ŹR£©£®
£Ø1£©Ö¤Ć÷²»ĀŪaĪŖŗĪŹµŹż£¬f£Øx£©¾łĪŖŌöŗÆŹż£»
£Ø2£©Čōf£Øx£©Āś×ćf£Ø©x£©+f£Øx£©=0£¬½ā¹ŲÓŚxµÄ²»µČŹ½f£Øx+1£©+f£Ø1©2x£©£¾0£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() ĪŖŹµ³£Źż.
ĪŖŹµ³£Źż.
£Ø1£©Éč![]() £¬µ±
£¬µ±![]() Ź±£¬ĒóŗÆŹż
Ź±£¬ĒóŗÆŹż![]() µÄµ„µ÷Ēų¼ä£»
µÄµ„µ÷Ēų¼ä£»
£Ø2£©µ±![]() Ź±£¬Ö±Ļß
Ź±£¬Ö±Ļß![]() ”¢
”¢![]() ÓėŗÆŹż
ÓėŗÆŹż![]() µÄĶ¼ĻóŅ»¹²ÓŠĖÄøö²»Ķ¬µÄ½»µć£¬ĒŅŅŌ“ĖĖĵćĪŖ¶„µćµÄĖıߊĪĒ”ĪŖĘ½ŠŠĖıߊĪ.ĒóÖ¤£ŗ
µÄĶ¼ĻóŅ»¹²ÓŠĖÄøö²»Ķ¬µÄ½»µć£¬ĒŅŅŌ“ĖĖĵćĪŖ¶„µćµÄĖıߊĪĒ”ĪŖĘ½ŠŠĖıߊĪ.ĒóÖ¤£ŗ ![]() .
.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬µćPŌŚÕż·½ŠĪABCDĖłŌŚĘ½ĆęĶā£¬PA”ĶĘ½ĆęABCD£¬PA=AB£¬ŌņPBÓėACĖł³ÉµÄ½ĒŹĒ£Ø £© 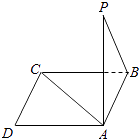
A.90”ć
B.60”ć
C.45”ć
D.30”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĘ½ĆęÉĻĮ½µćA£Ø©1£¬0£©£¬B£Ø1£¬0£©£¬ŌŚŌ²C£ŗ£Øx©3£©2+£Øy©4£©2=4ÉĻČ”Ņ»µćP£¬
£Ø¢ń£©x©y+c”Ż0ŗć³ÉĮ¢£¬ĒócµÄ·¶Ī§
£Ø¢ņ£©“Óx+y+1=0ÉĻµÄµćĻņŌ²ŅżĒŠĻߣ¬ĒóĒŠĻß³¤µÄ×īŠ”Öµ
£Ø¢ó£©Ēó|PA|2+|PB|2µÄ×īÖµ¼°“ĖŹ±µćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij°ąŃ§Éś½ųŠŠĮĖČż“ĪŹżŃ§²āŹŌ£¬µŚŅ»“ĪÓŠ8ĆūѧɜµĆĀś·Ö£¬µŚ¶ž“ĪÓŠ10ĆūѧɜµĆĀś·Ö£¬µŚČż“ĪÓŠ12ĆūѧɜµĆĀś·Ö£¬ŅŃÖŖĒ°Į½“Ī¾łĪŖĀś·ÖµÄѧɜӊ5Ćū£¬Čż“Ī²āŹŌÖŠÖĮÉŁÓÖŅ»“ĪµĆĀś·ÖµÄѧɜӊ15Ćū.ČōŗóĮ½“Ī¾łĪŖĀś·ÖµÄѧɜÖĮ¶ąÓŠ![]() Ćū£¬Ōņ
Ćū£¬Ōņ![]() µÄÖµĪŖ£Ø £©
µÄÖµĪŖ£Ø £©
A. 7 B. 8 C. 9 D. 10
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com