
(本小题13分) 如图所示, PQ为平面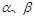 的交线, 已知二面角
的交线, 已知二面角 为直二面角,
为直二面角, 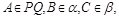
 , ∠BAP=45°.
, ∠BAP=45°.
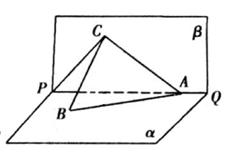
(1)证明: BC⊥PQ;
(2)设点C在平面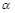 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
(3)当 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.
(1)证明见解析
(2)k=1
(3)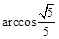
【解析】(1)在平面 内过点C作CE⊥PQ于点E, 由题知点E与点A不重合,
连接EB.
内过点C作CE⊥PQ于点E, 由题知点E与点A不重合,
连接EB.
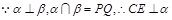 ,
即点C在平面
,
即点C在平面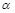 内的射影为点E,
内的射影为点E,
所以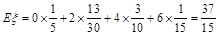 .
.
又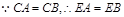 .
.
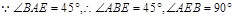 ,
故 BE⊥PQ, 又
,
故 BE⊥PQ, 又
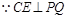 ,
,  ,
,
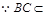 平面EBC, 故BC⊥PQ.
平面EBC, 故BC⊥PQ.
(2)由(1)知, O点即为E点, 设点F是O在平面ABC内的射影, 连 接BF并延长交AC于点D, 由题意可知, 若F是△ABC的重心, 则点D为AC的中点.
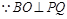 , 平面角
, 平面角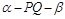 为直二面角,
为直二面角, 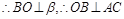 , 由三垂线定理可知AC⊥BF, 即AC⊥BD,
, 由三垂线定理可知AC⊥BF, 即AC⊥BD, 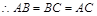 ,
即k=1;反之, 当k=1时, 三棱锥O—ABC为正三棱锥, 此时, 点O在平面ABC内的射影恰好为△ABC的重心.
,
即k=1;反之, 当k=1时, 三棱锥O—ABC为正三棱锥, 此时, 点O在平面ABC内的射影恰好为△ABC的重心.
(3)由(2)知, 可以O为原点, 以OB、OA、OC所在的直线为x轴、y轴、z轴建立空间直角坐标系O—xyz(如图所示)
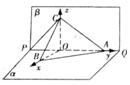
不妨设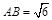 , 在Rt△OAB中, ∠ABO=∠BAO=45°,
所以BO=AO=
, 在Rt△OAB中, ∠ABO=∠BAO=45°,
所以BO=AO=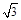 , 由CA=CB=kAB且
, 由CA=CB=kAB且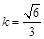 得, AC=2,
得, AC=2, 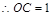 ,
则
,
则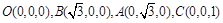 .
.
所以
设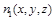 是平面ABC的一个法向量, 由
是平面ABC的一个法向量, 由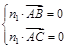 得
得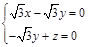
取x=1, 得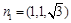
易知 是平面
是平面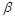 的一个法向量,
的一个法向量,
设二面角B-AC-P的平面角为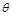 , 所以
, 所以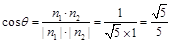 , 由图可知,
, 由图可知,
二面角B-AC-P的大小为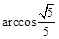 .
.


科目:高中数学 来源:2014届湖北武汉部分重点中学高二上学期期末考试文科数学卷(解析版) 题型:解答题
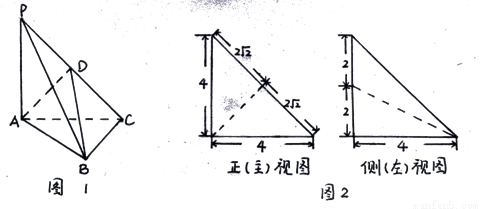
(本小题13分)如图1,在三棱锥P—ABC中, 平面ABC,
平面ABC, ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
(1)证明: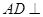 平面PBC;
平面PBC;
(2)求三棱锥D—ABC的体积;
(3)在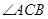 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得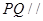 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题13分)如图,棱锥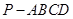 的底面
的底面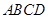 是矩形,
是矩形,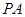 ⊥平面
⊥平面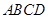 ,
,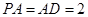 ,
,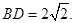
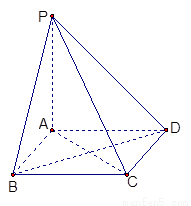
(1)求证: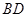 ⊥平面
⊥平面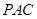 ;
;
(2)求二面角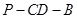 的大小;
的大小;
(3)求点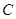 到平面
到平面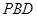 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2014届安徽宿松县复兴中学高一第二学期第三次月考数学试卷(解析版) 题型:解答题
(本小题13分)
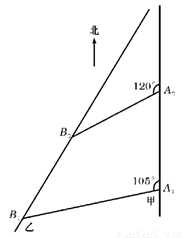
如图,甲船以每小时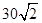 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于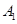 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西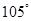 的方向
的方向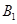 处,此时两船相距20海里.当甲船航行20分钟到达
处,此时两船相距20海里.当甲船航行20分钟到达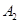 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西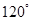 方向的
方向的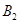 处,此时两船相距
处,此时两船相距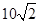 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区示范校高三第二学期综合练习数学文卷 题型:解答题
(本小题13分)如图,在四棱锥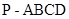 中,
中,
底面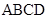 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面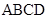 ,
,
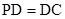 ,
,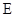 是
是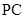 的中点,作
的中点,作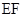 ⊥
⊥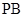 交
交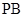 于点
于点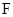 .
.
(1)证明: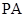 ∥平面
∥平面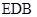 ;
;
(2)证明: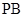 ⊥平面
⊥平面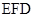 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
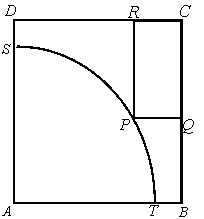
(本小题13分)如图![]() 是一块边长为100米的正方形地皮,其中
是一块边长为100米的正方形地皮,其中![]() 是一半径为90米的扇形小山,
是一半径为90米的扇形小山,![]() 是弧
是弧![]() 上一点,其余都是平地,现一开发商想在平地上建造一个有边落在
上一点,其余都是平地,现一开发商想在平地上建造一个有边落在![]() 与
与![]() 上的长方形停车场
上的长方形停车场![]() ,求长方形停车场的最大面积和最小面积。(请将结果精确到个位)【提示:
,求长方形停车场的最大面积和最小面积。(请将结果精确到个位)【提示:![]() 】
】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com