
【题目】已知函数![]() ,
,![]() ,曲线
,曲线![]() 与
与![]() 在原点处有公共切线.
在原点处有公共切线.
(I)若![]() 为函数的极大值点,求
为函数的极大值点,求![]() 的单调区间(用
的单调区间(用![]() 表示);
表示);
(II)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)首先分别求出![]() ,然后利用导数的几何意义求得
,然后利用导数的几何意义求得![]() ,由此对分
,由此对分![]() 、
、![]() 利用导数研究函数的单调性即可得出;(Ⅱ)首先利用导数得到函数
利用导数研究函数的单调性即可得出;(Ⅱ)首先利用导数得到函数![]() 的单调性,由此得到
的单调性,由此得到![]() 的最小值,从而得到
的最小值,从而得到![]() ,设
,设![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() ,利用导数研究函数的单调性即可得出.
,利用导数研究函数的单调性即可得出.
试题解析:(I)由题意知:![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,![]() ,
,
因为曲线![]() 与
与![]() 在原点处有公共的切线,故
在原点处有公共的切线,故![]() ,
,
解得:![]() ,………………2分
,………………2分
所以![]() ,
,
![]() .………………3分
.………………3分
![]() 时,
时,![]() ,函数
,函数![]() 在定义域上是减函数,故不满足题意;4分
在定义域上是减函数,故不满足题意;4分
![]() 时,因为
时,因为![]() 为函数
为函数![]() 的极大值点,故由
的极大值点,故由![]() 的图象可知
的图象可知![]() ,
,
由![]() 得:
得:![]() ,由
,由![]() 得:
得:![]() .
.
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() .………………6分
.………………6分
(II)因为![]() ,且
,且![]() 时
时![]() ,
,![]() 时
时![]() ,
,
故![]() 时,
时,![]() 取得最小值0,所以
取得最小值0,所以![]() ,即
,即![]() ,从而
,从而![]() .
.
设![]() ,
,
则![]() .………………7分
.………………7分
①当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() ,即
,即![]() ,所以
,所以![]() .………………9分
.………………9分
②当![]() 时,由①知
时,由①知![]() ,
,
所以![]() ,故
,故![]() ,即
,即![]() .……11分
.……11分
③当![]() 时,令
时,令![]() ,则
,则![]() ,
,
显然![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,![]() ,
,
所以![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
从而![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
从而当![]() 时,
时,![]() ,即
,即![]() ,不合题意.………………13分
,不合题意.………………13分
综上,实数![]() 的取值范围为
的取值范围为![]() .………………14分
.………………14分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
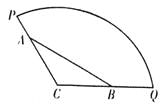
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在
处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在![]() 处的抽中率
处的抽中率![]() ,在
,在![]() 处的抽中率为
处的抽中率为![]() ,该同学选择现在
,该同学选择现在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
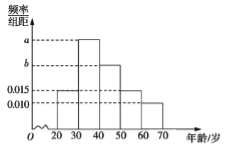
(1)已知中间三个年龄段的网上购票人数成等差数列,求![]() 的值;
的值;
(2)为鼓励大家网上购票,该平台常采用购票就发放酒店入住代金券的方法进行促销,具体做法如下:
年龄在![]() 岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
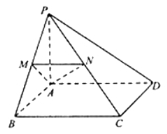
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:当点![]() 不与点
不与点![]() 重合时,
重合时,![]() 平面
平面![]() ;
;
(3)当![]() ,
,![]() 时,求点
时,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com