
【题目】设函数![]() 分别在
分别在![]() 、
、![]() 处取得极小值、极大值.
处取得极小值、极大值.![]() 平面上点
平面上点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,该平面上动点
,该平面上动点![]() 满足
满足![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点.
的对称点.
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
(Ⅱ)求动点![]() 的轨迹方程.
的轨迹方程.
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,点A(2,y0)为抛物线上一点,且|AF|=4.
(1)求抛物线的方程;
(2)直线l:y=x+m与抛物线交于不同两点P,Q,若![]() ,其中O为坐标原点,求m的值.
,其中O为坐标原点,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
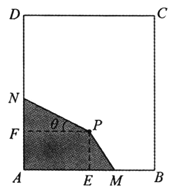
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇政府为了解决农村教师的住房问题,计划征用一块土地盖一幢建筑总面积为10000![]() 公寓楼(每层的建筑面积相同).已知士地的征用费为
公寓楼(每层的建筑面积相同).已知士地的征用费为![]() ,土地的征用面积为第一层的
,土地的征用面积为第一层的![]() 倍,经工程技术人员核算,第一层建筑费用为
倍,经工程技术人员核算,第一层建筑费用为![]() ,以后每增高一层,其建筑费用就增加
,以后每增高一层,其建筑费用就增加![]() ,设这幢公寓楼高层数为n,总费用为
,设这幢公寓楼高层数为n,总费用为![]() 万元.(总费用为建筑费用和征地费用之和)
万元.(总费用为建筑费用和征地费用之和)
(1)若总费用不超过835万元,求这幢公寓楼最高有多少层数?
(2)试设计这幢公寓的楼层数,使总费用最少,并求出最少费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记X表示学生的考核成绩,并规定X≥85为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图.
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足X![]() [70,79]的学生中任取3人,设Y表示这3人重成绩满足
[70,79]的学生中任取3人,设Y表示这3人重成绩满足![]() ≤10的人数,求Y的分布列和数学期望.
≤10的人数,求Y的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() ,则下列四个命题:
,则下列四个命题:

①点![]() 在直线
在直线![]() 上运动时,直线
上运动时,直线![]() 与直线
与直线![]() 所成角的大小不变
所成角的大小不变
②点![]() 在直线
在直线![]() 上运动时,直线
上运动时,直线![]() 与平面
与平面![]() 所成角的大小不变
所成角的大小不变
③点![]() 在直线
在直线![]() 上运动时,二面角
上运动时,二面角![]() 的大小不变
的大小不变
④点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积不变
的体积不变
其中的真命题是 ( )
A.①③B.③④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是真命题的是![]()
![]()
A. 命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
C. 命题p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
D. “![]() ”是“函数
”是“函数![]() 为偶函数”的充要条件
为偶函数”的充要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com