
分析 (1)若a=1,求出集合A,B,利用集合的基本运算即可求A∪B,(∁UA)∩B;
(2)若B⊆A,根据集合的基本关系,即可求实数a的取值范围.
解答 解:(1)若a=1,则A={x|1≤x≤2},B={x|$\frac{2}{3}$≤x≤2},
此时A∪B={x|1≤x≤2}∪{x|$\frac{2}{3}$≤x≤2}={x|$\frac{2}{3}$≤x≤2}.
由∁UA={x|x<1,或x>2},
∴(∁UA)∩B={x|x<1,或x>2}∩{x|$\frac{2}{3}$≤x≤2}={x|$\frac{2}{3}$≤x<1}.
(2)B={x|$\frac{2}{3}$≤x≤2},
又∵B⊆A,∴a≤$\frac{2}{3}$,
即实数a的取值范围是:a≤$\frac{2}{3}$.
点评 本题主要考查集合的基本运算,求出集合的等价条件是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
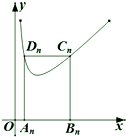 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{x}$(x>0)的图象上.若点Bn的坐为(n,0)(n≥2,n∈N+),记矩形AnBnCnDn的周长为an,则${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=( )
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{x}$(x>0)的图象上.若点Bn的坐为(n,0)(n≥2,n∈N+),记矩形AnBnCnDn的周长为an,则${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=( )| A. | 9×213 | B. | 9×214-32 | C. | 9×214-24 | D. | 9×213+24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩好 | ||
| C. | 甲、乙的成绩一样 | D. | 甲、乙的成绩无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
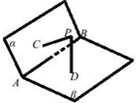 如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:
如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com