
【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为![]() (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
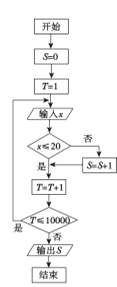
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A、B、C的对边分别是a,b,c,给出下列命题: ①若sinBcosC>﹣cosBsinC,则△ABC一定是钝角三角形;
②若sin2A+sin2B=sin2C,则△ABC一定是直角三角形;
③若bcosA=acosB,则△ABC为等腰三角形;
④在△ABC中,若A>B,则sinA>sinB;
其中正确命题的序号是 . (注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() ;
;
(2)设圆![]() 与
与![]() 轴的负半轴的交点为
轴的负半轴的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,试证明直线
,试证明直线![]() 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和Sn , 首项a1=a,公比为q(q≠0且q≠1).
(1)推导证明:Sn= ![]() ;
;
(2)等比数列{an}中,是否存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列?若存在,求出符合条件的等比数列公比q的值,若不存在,说明理由;
(3)本题中,若a=q=2,已知数列{nan}的前n项和Tn , 是否存在正整数n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.单位向量都相等
B.若 ![]() 与
与 ![]() 是共线向量,
是共线向量, ![]() 与
与 ![]() 是共线向量,则
是共线向量,则 ![]() 与
与 ![]() 是共线向量
是共线向量
C.| ![]() +
+ ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]()
![]() =0
=0
D.若 ![]() 与
与 ![]() 是单位向量,则
是单位向量,则 ![]()
![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=15,a3和a5的等差中项为9
(1)求an及Sn
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点与
的一个焦点与![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一顶点为
为对角线的菱形的一顶点为![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com