

| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
分析 连接DE,连接并延长EP交BC于点F,利用DE是△ABC中位线,求出FC=$\frac{1}{2}$BC,再用PQ是△EFC中位线,PQ=$\frac{1}{2}$CF,即可求得答案.
解答 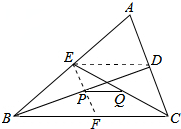 解:连接DE,连接并延长EP交BC于点F,
解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=$\frac{1}{2}$BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,∠EDB=∠DBF,DP=BP,∠EPD=∠BPF,
∴△DEP≌△BFP(ASA),
∴BF=DE=$\frac{1}{2}$BC,P是EF中点,
∴FC=$\frac{1}{2}$BC,
PQ是△EFC中位线,PQ=$\frac{1}{2}$FC,
∴PQ:BC=1:4.
故选:B.
点评 本题考查两线段比值的求法,是中档题,解题时要认真审题,注意三角形中位线定理的合理运用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组(分数) | 频数 | 频率 |
| [60,70) | 0.12 | |
| [70,80) | 20 | |
| [80,90) | 0.24 | |
| [90,100] | 12 | |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 12$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com