
【题目】已知函数![]()
![]() ,该函数所表示的曲线上的一个最高点为
,该函数所表示的曲线上的一个最高点为![]() ,由此最高点到相邻的最低点间曲线与
,由此最高点到相邻的最低点间曲线与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 函数解析式;
函数解析式;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求
,求![]() 的值域.
的值域.
【答案】(1) ![]() ;(2)
;(2)![]() 的单调增区间
的单调增区间![]() , 单调递减区间
, 单调递减区间![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由曲线y=Asin(ωx+φ)的一个最高点是![]() ,得A=
,得A=![]() ,又最高点
,又最高点![]() 到相邻的最低点间,曲线与x轴交于点(6,0),则
到相邻的最低点间,曲线与x轴交于点(6,0),则![]() =6-2=4,即T=16,所以ω=
=6-2=4,即T=16,所以ω=![]() .此时y=
.此时y=![]() sin(
sin(![]() x+φ),将x=2,y=
x+φ),将x=2,y=![]() 代入得
代入得![]() =
=![]() sin(
sin(![]() ×2+φ),
×2+φ),![]() ,
,![]() +φ=
+φ=![]() ,∴φ=
,∴φ=![]() ,所以这条曲线的解析式为
,所以这条曲线的解析式为![]() .
.
(2)因为![]() ∈[2kπ-
∈[2kπ-![]() ,2kπ+
,2kπ+![]() ],解得x∈[16k-6,2+16k],k∈Z.所以函数的单调增区间为[-6+16k,2+16k],k∈Z,因为
],解得x∈[16k-6,2+16k],k∈Z.所以函数的单调增区间为[-6+16k,2+16k],k∈Z,因为![]() ∈[2kπ+
∈[2kπ+![]() ,2kπ+
,2kπ+![]() ],解得x∈[2+16k,10+16k],k∈Z,
],解得x∈[2+16k,10+16k],k∈Z,
所以函数的单调减区间为:[2+16k,10+16k],k∈Z,
(3)因为![]() ,由(2)知函数f(x)在[0.2]上单调递增,在[2,8]上单调递减,所以当x=2时,f(x)有最大值为
,由(2)知函数f(x)在[0.2]上单调递增,在[2,8]上单调递减,所以当x=2时,f(x)有最大值为![]() ,当x=8时,f(x)有最小值为-1,故f(x)的值域为
,当x=8时,f(x)有最小值为-1,故f(x)的值域为![]()


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 若a1=1,且Sn=tan﹣ ![]() ,其中n∈N*.
,其中n∈N*.
(1)求实数t的值和数列{an}的通项公式;
(2)若数列{bn}满足bn=log3a2n , 求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
x | ﹣1 | 0 | 4 | 5 |
f(x) | 1 | 2 | 2 | 1 |
(1)函数y=f(x)是周期函数;
(2)函数f(x)在(0,2)上是减函数;
(3)如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
(4)当1<a<2时,函数y=f(x)﹣a有4个零点.
其中真命题的个数有( )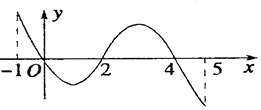
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市疾控中心流感监测结果显示,自![]() 年
年![]() 月起,该市流感活动一度出现上升趋势,尤其是
月起,该市流感活动一度出现上升趋势,尤其是![]() 月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知
月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知![]() 位同学中有
位同学中有![]() 位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
方案乙:先任取![]() 个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这
个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这![]() 位中的
位中的![]() 位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外
位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外![]() 位同学中逐个检测;
位同学中逐个检测;
(1)求依方案甲所需化验次数等于方案乙所需化验次数的概率;
(2)![]() 表示依方案甲所需化验次数,
表示依方案甲所需化验次数,![]() 表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元。
(1)设铁栅长为![]() 米,一堵砖墙长为
米,一堵砖墙长为![]() 米,求函数
米,求函数![]() 的解析式;
的解析式;
(2)为使仓库总面积![]() 达到最大,正面铁栅应设计为多长?
达到最大,正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}中,a1=2,且a2+1,a4+1,a8+1成等比数列.
(1)求数列{an}通项公式;
(2)设数列{bn}满足bn= ![]() ,求适合方程b1b2+b2b3+…+bnbn+1=
,求适合方程b1b2+b2b3+…+bnbn+1= ![]() 的正整数n的值.
的正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 其中P,M是非空数集,且P∩M=,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
其中P,M是非空数集,且P∩M=,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
(I)若P=(﹣∞,0),M=[0,4],求f(P)∪f(M);
(II)是否存在实数a>﹣3,使得P∪M=[﹣3,a],且f(P)∪f(M)=[﹣3,2a﹣3]?若存在,请求出满足条件的实数a;若不存在,请说明理由;
(III)若P∪M=R,且0∈M,I∈P,f(x)是单调递增函数,求集合P,M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于不等式![]() ,则对区间
,则对区间![]() 上的任意x都成立的实数t的取值范围是_______.
上的任意x都成立的实数t的取值范围是_______.
【答案】![]()
【解析】
根据二次函数的单调性求出x2﹣3x+2在区间[0,2]上的最小值和最大值,把问题转化关于t的不等式组 得答案.
得答案.
∵x2﹣3x+2=![]() ,
,
∴当x∈[0,2]时,![]() ,(x2﹣3x+2)max=2.
,(x2﹣3x+2)max=2.
∴ .
.
∴对于不等式![]() (2t﹣t2)≤x2﹣3x+2≤3﹣t2,对区间[0,2]上任意x都成立的实数t的取值范围是[﹣1,1﹣
(2t﹣t2)≤x2﹣3x+2≤3﹣t2,对区间[0,2]上任意x都成立的实数t的取值范围是[﹣1,1﹣![]() ].
].
故答案为:[﹣1,1﹣![]() ].
].
【点睛】
本题考查函数恒成立问题,考查了不等式的解法,体现了数学转化思想方法,是基础题.二次不等式分含参二次不等式和不含参二次不等式;对于含参的二次不等式问题,先判断二次项系数是否含参,接着讨论参数等于0,不等于0,再看式子能否因式分解,若能够因式分解则进行分解,再比较两根大小,结合图像得到不等式的解集.
【题型】填空题
【结束】
16
【题目】等差数列{an}的公差d≠0满足![]() 成等比数列,若
成等比数列,若![]() =1,Sn是{
=1,Sn是{![]() }的前n项和,则
}的前n项和,则![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com