
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)对任意的![]() ,
,![]() ,
,![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数![]() 的一种方法.例如:3可表示为“
的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用
”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用![]() 这9数字表示两位数的个数为
这9数字表示两位数的个数为![]()
![]()
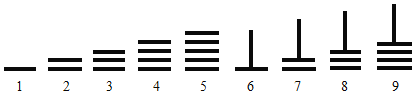
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,椭圆
为其焦点,椭圆![]() ,
,![]() ,
,![]() 为其左右焦点,离心率
为其左右焦点,离心率![]() ,过
,过![]() 作
作![]() 轴的平行线交椭圆于
轴的平行线交椭圆于![]() 两点,
两点,![]() .
.
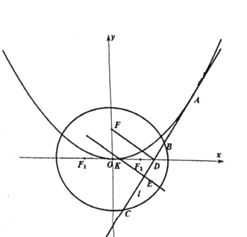
(1)求椭圆的标准方程;
(2)过抛物线上一点![]() 作切线
作切线![]() 交椭圆于
交椭圆于![]() 两点,设
两点,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中垂线交
的中垂线交![]() 轴为
轴为![]() ,
,![]() ,
,![]() 的面积分别记为
的面积分别记为![]() ,
,![]() ,若
,若![]() ,且点
,且点![]() 在第一象限.求点
在第一象限.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地的中小学办学条件在政府的教育督导下,迅速得到改变.教育督导一年后.分别随机抽查了初中(用![]() 表示)与小学(用
表示)与小学(用![]() 表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为( )(80分及以上为优秀). ①初中得分与小学得分的优秀率相同;②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.
表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为( )(80分及以上为优秀). ①初中得分与小学得分的优秀率相同;②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.

A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】条形码是由一组规则排列的条、空及其对应的代码组成,用来表示一定的信息,我们通常见的条形码是“![]() ”通用代码,它是由从左到右排列的
”通用代码,它是由从左到右排列的![]() 个数字(用
个数字(用![]() ,
,![]() ,…,
,…,![]() 表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中
表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中![]() 是校验码,用来校验前
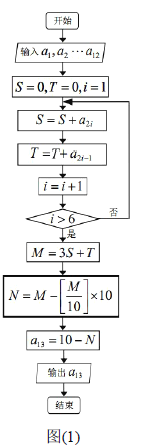
是校验码,用来校验前![]() 个数字代码的正确性.图(1)是计算第
个数字代码的正确性.图(1)是计算第![]() 位校验码的程序框图,框图中符号
位校验码的程序框图,框图中符号![]() 表示不超过
表示不超过![]() 的最大整数(例如
的最大整数(例如![]() ).现有一条形码如图(2)所示(
).现有一条形码如图(2)所示(![]() ),其中第
),其中第![]() 个数被污损,那么这个被污损数字
个数被污损,那么这个被污损数字![]() 是( )
是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com