
【题目】已知![]()
(1)证明函数f ( x )的图象关于![]() 轴对称;
轴对称;
(2)判断![]() 在
在![]() 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(3)当x∈[1,2]时函数f (x )的最大值为![]() ,求此时a的值。
,求此时a的值。
【答案】(1)证明见解析;(2)答案见解析;(3) ![]() ,或
,或![]()
【解析】试题分析:(1)定义域为![]() ,证明
,证明![]() ,确定函数为偶函数,从而证得函数
,确定函数为偶函数,从而证得函数![]() 的图象关于
的图象关于![]() 轴对称;(2)利用单调性的定义,设
轴对称;(2)利用单调性的定义,设![]() ,作差
,作差![]() ,化简确定差的正负,从而证得函数的单调性;(3)根据(2)的结论,利用函数的单调性,即可得到函数的最大值,再根据函数的最大值为
,化简确定差的正负,从而证得函数的单调性;(3)根据(2)的结论,利用函数的单调性,即可得到函数的最大值,再根据函数的最大值为![]() ,列出等式,即可求得
,列出等式,即可求得![]() 的值.
的值.
试题解析:(1)要证明函数![]() 的图象关于
的图象关于![]() 轴对称,只须证明函数
轴对称,只须证明函数![]() 是偶函数
是偶函数
∵![]() ,由
,由![]()
∴函数![]() 是偶函数,即函数
是偶函数,即函数![]() 的图象关于
的图象关于![]() 轴对称
轴对称
(2).证明:任取![]() 且
且![]() ,因为
,因为
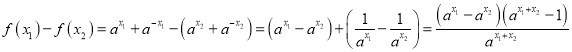 ,
,
①当![]() 时,由0<
时,由0<![]() ,则
,则![]() ,则
,则![]() .
.![]() .
.![]() .
.![]() ;
;
![]() <0即
<0即![]() ;
;
②当![]() 时,由0<
时,由0<![]() ,则x1+x2>0,则
,则x1+x2>0,则![]() .
.![]() .
.![]() .
.![]() ;
; ![]() 即
即![]() ;
;
所以,对于任意![]() (
(![]() ),f(x)在
),f(x)在![]() 上都为增函数。
上都为增函数。
(3)由(2)知![]() 在
在![]() 上为增函数,则当
上为增函数,则当![]() 时,函数
时,函数![]() 亦为增函数;
亦为增函数;
由于函数![]() 的最大值为
的最大值为![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ,或
,或![]()


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=![]() ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”为真命题;
≥1”为真命题;
而“对任意的正数x,2x+![]() ≥1的”时,可得“a≥
≥1的”时,可得“a≥![]() ”
”
即“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”为假命题;
”为假命题;
故“a=![]() ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+![]() ≥1的”充分不必要条件
≥1的”充分不必要条件
故选A
【题型】单选题
【结束】
9
【题目】如图是一几何体的平面展开图,其中![]() 为正方形,
为正方形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,在此几何体中,给出下面四个结论:①直线
的中点,在此几何体中,给出下面四个结论:①直线![]() 与直线
与直线![]() 异面;②直线
异面;②直线![]() 与直线
与直线![]() 异面;③直线
异面;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .
.
其中一定正确的选项是( )

A. ①③ B. ②③ C. ②③④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级实验班与普通班共1000名学生,其中实验班学生200人,普通班学生800人,现将高三一模考试数学成绩制成如图所示频数分布直方图,按成绩依次分为5组,其中第一组([0, 30)),第二组([30, 60)),第三组([60, 90)),的频数成等比数列,第一组与第五组([120, 150))的频数相等,第二组与第四组([90, 120))的频数相等。
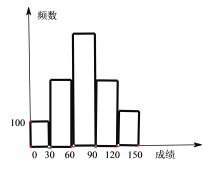
(1)求第三组的频率;
(2)已知实验班学生成绩![]() 在第五组,
在第五组,![]() 在第四组,剩下的都在第三组,试估计实验班学生数学成绩的平均分;
在第四组,剩下的都在第三组,试估计实验班学生数学成绩的平均分;
(3)在(2)的条件下,按分层抽样的方法从第5组中抽取5人进行经验交流,再从这5人中随机抽取3人在全校师生大会上作经验报告,求抽取的3人中恰有一个普通班学生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的一个顶点为A(0,-1),焦点在x轴上。若右焦点F到直线x-y+2![]() =0的距离为3。
=0的距离为3。
(1)求椭圆的方程;
(2)设直线y=kx+m(k≠0)与椭圆相交于不同的两点M、N。当|AM|=|AN|时,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 是
是![]() 的菱形,侧面
的菱形,侧面![]() 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面![]() .
.

(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() 为边
为边![]() 的中点,能否在棱
的中点,能否在棱![]() 上找到一点
上找到一点![]() ,使平面
,使平面![]() 平面
平面![]() ?并证明你的结论.
?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(![]() )若已知方程表示椭圆,则
)若已知方程表示椭圆,则![]() 的取值范围为__________.
的取值范围为__________.
(![]() )语句“
)语句“![]() ”是语句“方程
”是语句“方程![]() ”表示双曲线的(_____________).
”表示双曲线的(_____________).
A.充分不必要条件 B.必要不充分条件 C.充在条件 D.既不充分也不必要条件
(![]() )根据(
)根据(![]() )的结论,以“如果
)的结论,以“如果![]() 那么
那么![]() ”的形式写出一个正确命题,记作命题
”的形式写出一个正确命题,记作命题![]() ,则
,则
命题![]() :__________.
:__________.
(![]() )套用量词命题的格式:“
)套用量词命题的格式:“![]() ,
, ![]() ”或“
”或“![]() ,
, ![]() ”,改写(
”,改写(![]() )中命题
)中命题![]() ,
,
表述形式为:__________.
(![]() )写出(
)写出(![]() )中命题
)中命题![]() 的逆命题,记作命题
的逆命题,记作命题![]() ,则
,则
命题![]() :__________.
:__________.
(![]() )判断(
)判断(![]() )中命题
)中命题![]() 的真假,并陈述判断理由.
的真假,并陈述判断理由.
![]() 命题为__________命题,因为__________.
命题为__________命题,因为__________.
(![]() )若已知方程表示椭圆,则该椭圆两个焦点的坐标分别为__________.
)若已知方程表示椭圆,则该椭圆两个焦点的坐标分别为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x+![]() ), (x∈R)有下列命题:
), (x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
② y=f(x)可改写为y=4cos(2x-![]() );
);
③y=f(x)的图象关于(-![]() ,0)对称;
,0)对称;
④ y=f(x)的图象关于直线x=-![]() 对称;
对称;
其中正确的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com