
【题目】已知函数f(x)=lg ![]() 的定义域为集合A,函数g(x)=
的定义域为集合A,函数g(x)= ![]() 的定义域为集合B.
的定义域为集合B.
(1)求集合A,B;
(2)若AB,求实数a的取值范围.
【答案】
(1)解:由 ![]() >0,可得1<x<2,∴A={x|1<x<2};
>0,可得1<x<2,∴A={x|1<x<2};
由2x﹣a≥0,可得x≥ ![]() ,∴B={x|x≥
,∴B={x|x≥ ![]() }
}
(2)解:∵AB,∴ ![]() ≤1,∴a≤2
≤1,∴a≤2
【解析】(1)根据对数、二次根式有意义的条件求集合A,B;(2)若AB,建立不等式求实数a的取值范围.
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是递增的等差数列,前n项和为Sn , a1=1,且a1 , a2 , S3成等比数列.
(1)求an及Sn;
(2)求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一生物科研小组对升高温度的多少与某种细菌种群存活数量之间的关系进行分析研究,他们制作5 份相同的样本并编号1、2、3、4、5,分别记录它们同在![]() 下升高不同的温度后的种群存活数量, 得到如下资料:
下升高不同的温度后的种群存活数量, 得到如下资料:
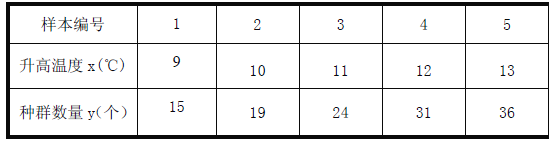
(1)若随机选取2份样本的数据来研究,求其编号不相邻的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)利用(2)中所求出的回归方程预测温度升高15 ![]() 时此种样本中种菌群存活数量.
时此种样本中种菌群存活数量.
附: 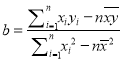 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3位进行其他方面的排查,其中患胃病的人数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
参考公式: 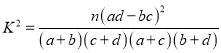 ,其中
,其中![]() .
.
下面的临界值仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣
x3﹣ ![]() (a∈R).
(a∈R).
(1)若a=1,求函数f(x)在[0,2]上的最大值;
(2)若对任意x∈(0,+∞),有f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com