
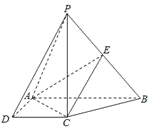
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,点
,点![]() ,动圆
,动圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (
(![]() 均不同于点
均不同于点![]() ),且
),且![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)证明:![]() 为定值,并求
为定值,并求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,当
两点,当![]() 三点共线时,求四边形
三点共线时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)已知![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)对于在![]() 中的任意一个常数
中的任意一个常数![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
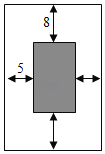
【题目】淄博七中、临淄中学为了加强交流,增进友谊,两校准备举行一场足球赛,由淄博七中版画社的同学设计一幅矩形宣传画,要求画面面积为![]() ,画面的上、下各留
,画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
空白.如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)已知在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标,曲线
轴正半轴为极轴建立极坐标,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )

A.120种B.240种C.144种D.288种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com