
【题目】设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 为偶函数时,求函数
为偶函数时,求函数![]() 的极值;
的极值;
(Ⅱ)若函数![]() 在区间
在区间![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)极小值![]() ,极大值
,极大值![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)根据偶函数定义列方程,解得![]() .再求导数,根据导函数零点列表分析导函数符号变化规律,即得极值,(Ⅱ)先分离变量,转化研究函数
.再求导数,根据导函数零点列表分析导函数符号变化规律,即得极值,(Ⅱ)先分离变量,转化研究函数![]() ,
,![]() ,利用导数研究
,利用导数研究![]() 单调性与图象,最后根据图象确定满足条件的
单调性与图象,最后根据图象确定满足条件的![]() 的取值范围.
的取值范围.
(Ⅰ)由函数![]() 是偶函数,得
是偶函数,得![]() ,
,
即![]() 对于任意实数
对于任意实数![]() 都成立,
都成立,
所以![]() .
.
此时![]() ,则
,则![]() .
.
由![]() ,解得
,解得![]() .
.
当x变化时,![]() 与
与![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
所以![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() 有极小值
有极小值![]() ,
,![]() 有极大值
有极大值![]() .
.
(Ⅱ)由![]() ,得
,得![]() . 所以“
. 所以“![]() 在区间
在区间![]() 上有两个零点”等价于“直线
上有两个零点”等价于“直线![]() 与曲线
与曲线![]() ,
,![]() 有且只有两个公共点”.
有且只有两个公共点”.
对函数![]() 求导,得
求导,得![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
当x变化时,![]() 与
与![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
所以![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 或
或![]() 时,直线
时,直线![]() 与曲线
与曲线![]() ,
,![]() 有且只有两个公共点.
有且只有两个公共点.
即当![]() 或
或![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.


科目:高中数学 来源: 题型:
【题目】随着“北京八分钟”在韩国平昌冬奥会惊艳亮相,冬奥会正式进入了北京周期,全社会对冬奥会的热情空前高涨.
(1)为迎接冬奥会,某社区积极推动冬奥会项目在社区青少年中的普及,并统计了近五年来本社区冬奥项目青少年爱好者的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年),列表如下:
(单位:年),列表如下:

依据表格给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).
并加以说明(计算结果精确到0.01).
(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式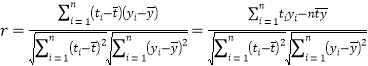 ,参考数据
,参考数据![]() .
.
(2)某冰雪运动用品专营店为吸引广大冰雪爱好者,特推出两种促销方案.
方案一:每满600元可减100元;
方案二:金额超过600元可抽奖三次,每次中奖的概率同为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
两位顾客都购买了1050元的产品,并且都选择第二种优惠方案,求至少有一名顾客比选择方案一更优惠的概率;
②如果你打算购买1000元的冰雪运动用品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 过点
过点![]() 且与直线
且与直线![]() 垂直,直线
垂直,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,动点
轴对称,动点![]() 满足
满足![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,问
,问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数之差为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海市旅游节刚落下帷幕,在旅游节期间,甲、乙、丙三位市民顾客分别获得一些景区门票的折扣消费券,数量如表1,已知这些景区原价和折扣价如表2(单位:元).
表1:
数量 | 景区1 | 景区2 | 景区3 |
甲 | 0 | 2 | 2 |
乙 | 3 | 0 | 1 |
丙 | 4 | 1 | 0 |
表2:
门票 | 景区1 | 景区2 | 景区3 |
原价 | 60 | 90 | 120 |
折扣后价 | 40 | 60 | 80 |
(1)按照上述表格的行列次序分别写出这三位市民获得的折扣消费券数量矩阵A和三个景区的门票折扣后价格矩阵B;
(2)利用你所学的矩阵知识,计算三位市民各获得多少元折扣?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a表示.

(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值,求图中a的所有可能取值;
(Ⅱ)将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设![]() ,现从所有的“阅读达人”里任取2人,求至少有1人来自甲组的概率;
,现从所有的“阅读达人”里任取2人,求至少有1人来自甲组的概率;
(Ⅲ)记甲组阅读量的方差为![]() . 若在甲组中增加一个阅读量为10的学生,并记新得到的甲组阅读量的方差为
. 若在甲组中增加一个阅读量为10的学生,并记新得到的甲组阅读量的方差为![]() ,试比较
,试比较![]() ,
,![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
(注:![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 与抛物线
与抛物线![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(1)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(2)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值
面积的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com