
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 圆心为
圆心为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(![]() )求
)求![]() 的取值范围;
的取值范围;
(![]() )是否存在常数
)是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
【答案】(1)![]() ;(2)不存在.
;(2)不存在.
【解析】试题分析:(1)圆的方程可得圆心为![]() ,半径为2,圆的面积为
,半径为2,圆的面积为![]() ,设直线l的方程为y=kx+2.直线l与圆
,设直线l的方程为y=kx+2.直线l与圆![]() 交于两个不同的点A,B等价于
交于两个不同的点A,B等价于![]() <2,解不等式即可求出结果.(2)设
<2,解不等式即可求出结果.(2)设![]() ,则
,则![]() +
+![]() ,由
,由![]()
得![]() ,根据韦达定理和共线定理,即可解得
,根据韦达定理和共线定理,即可解得![]() .由(2)知
.由(2)知![]() ,故可判断
,故可判断![]() 的情况.
的情况.
试题解析:(1)圆的方程可化为![]() ,可得圆心为
,可得圆心为![]() ,半径为2,故圆的面积为
,半径为2,故圆的面积为![]() .
.
设直线l的方程为y=kx+2.直线l与圆![]() 交于两个不同的点A,B等价于
交于两个不同的点A,B等价于![]() <2,化简得
<2,化简得![]() ,解得
,解得![]() ,即k的取值范围为
,即k的取值范围为![]() .
.
(2)设![]() ,则
,则![]() +
+![]() =(x1+x2,y1+y2),由
=(x1+x2,y1+y2),由![]()
得![]() ,
,
解此方程得x1,2=![]() .
.
则![]() -
-![]() ,①
,①
又![]() .②
.②
而![]() ,
,![]() =(6,-2).
=(6,-2).
所以![]() +
+![]() 与
与![]() 共线等价于
共线等价于![]() ,将①②代入上式,解得
,将①②代入上式,解得![]() .由(2)知
.由(2)知![]() ,故没有符合题意的常数
,故没有符合题意的常数![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.a∈R,“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0”
D.命题p:“?x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2 ![]() ﹣sinBsinC=
﹣sinBsinC= ![]() .
.
(1)求A;
(2)若a=4,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.

求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,且
,且![]() ,设命题
,设命题![]() :函数
:函数![]() 在
在![]() 上单调递减;命题
上单调递减;命题![]() :函数
:函数![]() 在
在![]() 上为增函数,
上为增函数,
(1)若“![]() 且
且![]() ”为真,求实数
”为真,求实数![]() 的取值范围
的取值范围
(2)若“![]() 且
且![]() ”为假,“
”为假,“![]() 或
或![]() ”为真,求实数
”为真,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共13分)
以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
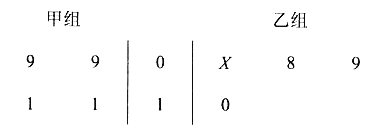
(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率。
(注:方差![]() 其中
其中![]() 为
为![]() ,
,![]() ,
,![]()
![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中所有正确命题的序号为______.
![]() 若方程
若方程![]() 表示圆,那么实数
表示圆,那么实数![]() ;
;
![]() 已知函数
已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,令
对称,令![]() ,则
,则![]() 的图象关于原点对称;
的图象关于原点对称;
![]() 在正方体
在正方体![]() 中,E、F分别是AB和
中,E、F分别是AB和![]() 的中点,则直线CE、
的中点,则直线CE、![]() F、DA三线共点;
F、DA三线共点;
![]() 幂函数的图象不可能经过第四象限.
幂函数的图象不可能经过第四象限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这些样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com