
给出四个命题:①存在实数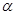 ,使
,使 ;②存在实数
;②存在实数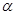 ,使
,使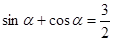 ;③
;③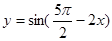 是偶函数;④
是偶函数;④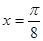 是函数
是函数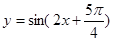 的一条对称轴方程;⑤若
的一条对称轴方程;⑤若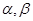 是第一象限角,且
是第一象限角,且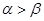 ,则
,则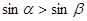 。其中所有的正确命题的序号是___ _.
。其中所有的正确命题的序号是___ _.
③②
【解析】
试题分析:对于①,利用二倍角的正弦公式变形,可得sinα?cosα的最大值为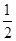 不成立
不成立
对于②,利用诱导公式化简为y=-cosx,该函数是偶函数;对于③,把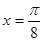 代入
代入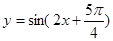 ,看y能否取得最值,若能取得最值,命题正确,否则,命题不正确;对于④举反例取α=
,看y能否取得最值,若能取得最值,命题正确,否则,命题不正确;对于④举反例取α=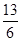 π,β=
π,β=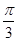 ,α、β是第一象限的角,且α>β,但sinα<sinβ,∴命题④错误.加以说明.通过以上分析即可得到正确答案,故可知正确的命题序号为③②
,α、β是第一象限的角,且α>β,但sinα<sinβ,∴命题④错误.加以说明.通过以上分析即可得到正确答案,故可知正确的命题序号为③②
考点:命题的真假判断,三角函数的性质
点评:本题考查了命题的真假判断与应用,考查了三角函数的被角公式、诱导公式及三角函数的性质,考查了举反例法在判断命题真假中的应用,此题是基础题.


科目:高中数学 来源: 题型:
| π |
| 8 |
| 5π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 8 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| π |
| 8 |
| 5 |
| 4 |
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com