
【题目】已知函数![]() .
.
(1)求证:当![]() 时,对任意
时,对任意![]() 恒成立;
恒成立;
(2)求函数![]() 的极值;
的极值;
(3)当![]() 时,若存在
时,若存在![]() 且
且![]() ,满足
,满足![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析 (2)极小值![]() ,无极大值. (3)见解析
,无极大值. (3)见解析
【解析】
(1)求导得到![]() ,即
,即![]() ,函数单调递增,得到证明.
,函数单调递增,得到证明.
(2)![]() ,讨论
,讨论![]() 和
和![]() 两种情况,分别计算极值得到答案.
两种情况,分别计算极值得到答案.
(3)![]() 在
在![]() 上为增函数,当
上为增函数,当![]() 时不成立,不防设
时不成立,不防设![]()
![]() ,计算得到
,计算得到![]() ,
,![]() 即证
即证![]() ,设
,设![]() ,只需证
,只需证![]() ,计算最值得到证明.
,计算最值得到证明.
(1)![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,
所以当![]() 时,恒有
时,恒有![]() 成立;
成立;
(2)由![]()
当![]()
![]() 在
在![]() 上为增函数,无极值
上为增函数,无极值
当![]()
![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
![]() 有极小值
有极小值![]() ,无极大值,
,无极大值,
综上知:当![]() 无极值,
无极值,
当![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
(3)当![]() 在
在![]() 上为增函数,
上为增函数,
由(2)知,当![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
这时,![]() 在
在![]() 上为增函数,
上为增函数,
所以不可能存在![]() ,
,
满足![]() 且
且![]()
所以有![]()
现不防设![]() 得:
得:
![]()
![]() ①
①
![]()
![]() ②
②
由①②式可得:![]()
即![]()
又![]()
![]() ③
③
又要证![]() 即证
即证![]()
![]()
即证![]() ……④
……④
所以由③式知,只需证明:![]() 即证
即证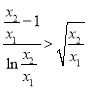
设![]() ,只需证
,只需证![]() ,即证:
,即证:![]()
令![]()
由 在
在![]() 上为增函数,
上为增函数,
![]()
![]() 成立,
成立,
所以由③知,![]() 成立,
成立,
所以![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,3次中至少两次投中8环以上的为优秀.现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投镖未在8环以上,用1表示该次投镖在8环以上;再以每三个随机数作为一组,代表一轮的结果.例如:“101”代表第一次投镖在8环以上,第二次投镖未在8环以上,第三次投镖在8环以上,该结果代表这一轮投镖为优秀:"100”代表第一次投镖在8环以上,第二次和第三次投镖均未在8环以上,该结果代表这一轮投镖为不优秀.经随机模拟实验产生了如下10组随机数,据此估计,该选手投掷飞镖两轮,至少有一轮可以拿到优秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+blnx(a,b∈R)在点(1,f(1))处的切线方程为y![]() x﹣1.
x﹣1.
(1)求ab的值;
(2)当x>1时,f(x)![]() 0恒成立,求实数k的取值范围;
0恒成立,求实数k的取值范围;
(3)设g(x)=ex![]() x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 内有两个极值点,求负数
内有两个极值点,求负数![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,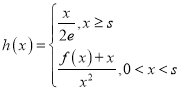 ,若对任意实数
,若对任意实数![]() ,总存在正实数
,总存在正实数![]() ,使得
,使得![]() 成立,求正实数
成立,求正实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 的首项
的首项![]() .
.
(1)如果![]() ,写出数列
,写出数列![]() 的通项公式;
的通项公式;
(2)如果![]() (
(![]() 且
且![]() ),要使得数列
),要使得数列![]() 是等差数列,求首项
是等差数列,求首项![]() 的取值范围;
的取值范围;
(3)如果![]() (
(![]() 且
且![]() ),求出数列
),求出数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com