
【题目】已知数列{an},{bn}都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列{cn}.
(1)设数列{an},{bn}分别为等差、等比数列,若a1=b1=1,a2=b3 , a6=b5 , 求c20;
(2)设{an}的首项为1,各项为正整数,bn=3n , 若新数列{cn}是等差数列,求数列{cn} 的前n项和Sn;
(3)设bn=qn﹣1(q是不小于2的正整数),c1=b1 , 是否存在等差数列{an},使得对任意的n∈N* , 在bn与bn+1之间数列{an}的项数总是bn?若存在,请给出一个满足题意的等差数列{an};若不存在,请说明理由.
【答案】
(1)解:设等差数列{an}的公差为d,等比数列{bn}的公比为q,
由题意得, ![]() ,解得d=0或3,因数列{an},{bn}单调递增,
,解得d=0或3,因数列{an},{bn}单调递增,
所以d>0,q>1,
所以d=3,q=2,
所以an=3n﹣2,bn=2n﹣1.
因为a1=b1=1,a2=b3,a6=b5,b7>a20.
∴c20=a17=49.
(2)解:设等差数列{cn}的公差为d,又a1,且bn=3n,
所以c1=1,所以cn=dn+1﹣d.
因为b1=3是{cn}中的项,所以设b1=cn,即d(n﹣1)=2.
当n≥4时,解得d= ![]() <1,不满足各项为正整数;
<1,不满足各项为正整数;
当b1=c3=3时,d=1,此时cn=n,只需取an=n,而等比数列{bn}的项都是等差数列{an},中的项,所以Sn= ![]() ;
;
当b1=c2=3时,d=2,此时cn=2n﹣1,只需取an=2n﹣1,
由3n=2m﹣1,得m= ![]() ,3n是奇数,3n+1 是正偶数,m有正整数解,
,3n是奇数,3n+1 是正偶数,m有正整数解,
所以等比数列{bn}的项都是等差数列{an}中的项,所以Sn=n2.
综上所述,数列{cn}的前n项和Sn= ![]() ,或Sn=n2.
,或Sn=n2.
(3)解:存在等差数列{an},只需首项a1∈(1,q),公差d=q﹣1…
下证bn与bn+1之间数列{an}的项数为bn.即证对任意正整数n,都有 ![]() ,
,
即 ![]() 成立.
成立.
由bn﹣ ![]() =qn﹣1﹣a1﹣(1+q+…+qn﹣2)(q﹣1)=1﹣a1<0,
=qn﹣1﹣a1﹣(1+q+…+qn﹣2)(q﹣1)=1﹣a1<0,
bn+1﹣ ![]() =qn﹣a1﹣(1+q+…+qn﹣1﹣1)(q﹣1)=q﹣a1>0..
=qn﹣a1﹣(1+q+…+qn﹣1﹣1)(q﹣1)=q﹣a1>0..
所以首项a1∈(1,q),公差d=q﹣1的等差数列{an}符合题意
【解析】(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,由题意得, ![]() ,解得d=0或3,因数列{an},{bn}单调递增,d>0,q>1,可得an=3n﹣2,bn=2n﹣1 , 利用通项公式即可得出.(2)设等差数列{cn}的公差为d,又a1 , 且bn=3n , 所以c1=1,所以cn=dn+1﹣d.因为b1=3是{cn}中的项,所以设b1=cn , 即d(n﹣1)=2.当n≥4时,解得d=
,解得d=0或3,因数列{an},{bn}单调递增,d>0,q>1,可得an=3n﹣2,bn=2n﹣1 , 利用通项公式即可得出.(2)设等差数列{cn}的公差为d,又a1 , 且bn=3n , 所以c1=1,所以cn=dn+1﹣d.因为b1=3是{cn}中的项,所以设b1=cn , 即d(n﹣1)=2.当n≥4时,解得d= ![]() <1,不满足各项为正整数当b1=c3=3时,当b1=c2=3时,即可得出.(3)存在等差数列{an},只需首项a1∈(1,q),公差d=q﹣1.下证bn与bn+1之间数列{an}的项数为bn . 即证对任意正整数n,都有
<1,不满足各项为正整数当b1=c3=3时,当b1=c2=3时,即可得出.(3)存在等差数列{an},只需首项a1∈(1,q),公差d=q﹣1.下证bn与bn+1之间数列{an}的项数为bn . 即证对任意正整数n,都有 ![]() ,作差利用通项公式即可得出.
,作差利用通项公式即可得出.
【考点精析】解答此题的关键在于理解数列的通项公式的相关知识,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两组各有三名同学,他们在一次测试中的成绩分别为:甲组:88、89、90;乙组:87、88、92.如果分别从甲、乙两组中随机选取一名同学,则这两名同学的成绩之差的绝对值不超过3的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某互联网大会上,为了提升安全级别,将5名特警分配到3个重要路口执勤,每个人只能选择一个路口,每个路口最少1人,最多3人,且甲和乙不能安排在同一个路口,则不同的安排方法有( )
A. 180种 B. 150种 C. 96种 D. 114种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年俄罗斯世界杯激战正酣,某校工会对全校教职工在世界杯期间每天收看比赛的时间作了一次调查,得到如下频数分布表:
收看时间 (单位:小时) |
|
|
|
|
|
|
| 14 |
|
| 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“球迷”,否则定义为“非球迷”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
球迷 | 40 | ||
非球迷 |
| ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“球迷”与“性别”有关;
(2)在全校“球迷”中按性别分层抽样抽取6名,再从这6名“球迷”中选取2名世界杯知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.其图象开口向上,且始终与![]() 轴有两个不同的交点
轴有两个不同的交点
B.无论![]() 取何实数,其图象始终过定点
取何实数,其图象始终过定点![]()
C.其图象对称轴的位置没有确定,但其形状不会因![]() 的取值不同而改变
的取值不同而改变
D.函数的最小值大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为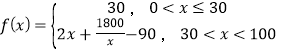 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2. 
(1)求证:BE∥平面PAD;
(2)求证:BC⊥平面PBD;
(3)在线段PC上是否存在一点Q,使得二面角Q﹣BD﹣P为45°?若存在,求 ![]() 的值;若不存在,请述明理由.
的值;若不存在,请述明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com