
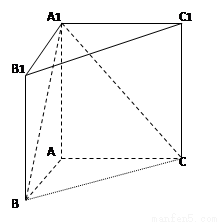
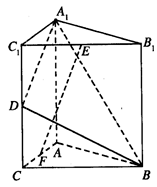
(13分) 如图,直三棱柱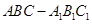 中,
中,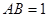 ,
,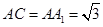 ,
,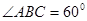 .
.
(Ⅰ)证明: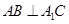 ;
;
(Ⅱ)求二面角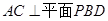
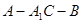 的正切值.
的正切值.
(Ⅰ)证明见解析;(Ⅱ)二面角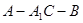 的正切值为
的正切值为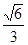 。
。
【解析】(I)证明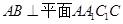 即可.
即可.
(II)过A作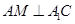 于M,连接BM,则易证
于M,连接BM,则易证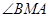 就是二面角
就是二面角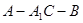 的平面角,然后解
的平面角,然后解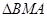 求角即可.
求角即可.
证明(Ⅰ)
∵三棱柱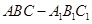 为直三棱柱
为直三棱柱
∴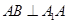 …………………………………1
…………………………………1
在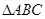 中
中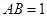
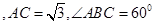
由正弦定理得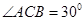 ……………………….3
……………………….3
∴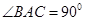 ……………………………………4
……………………………………4
即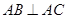 ,又
,又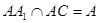
∴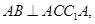 …………………………………….5
…………………………………….5
又因为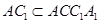
∴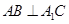 ………………………………………….6
………………………………………….6
(Ⅱ)作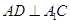 交
交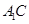 于
于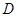 ,连
,连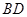 ,……………………7
,……………………7
由三垂线定理可得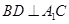 ……………………………………..9
……………………………………..9
所以∠ADB为二面角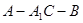 的平面角…………………….10
的平面角…………………….10
在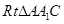 中,
中,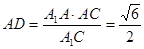 ,………………………..11
,………………………..11
在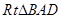 中,
中, ,
,
∴二面角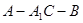 的正切值为
的正切值为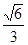 ……………………………13
……………………………13


科目:高中数学 来源: 题型:
(本小题满分13分)
如图在直三棱柱ABC—A1B1C1中,AC=BC=2,AA1=![]() ,∠ACB=90°,M是AA1的中点,N是BC1的中点。
,∠ACB=90°,M是AA1的中点,N是BC1的中点。
(1)求证:MN∥平面A1B1C1
|
(3)求二面角B-C1M—A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
 (本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上期中文科数学试卷(解析版) 题型:解答题
(本小题满分13分)
如图,在直三棱柱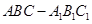 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中, 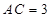 ,
,
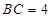 ,
,
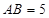 ,
,
 ,点
,点 是
是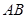 的中点.
的中点.

(Ⅰ)
求证: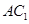 ∥平面
∥平面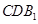 ;
;
(Ⅱ)求AC1与平面CC1B1B所成的角.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学理工类模拟试卷(三) 题型:解答题
(本小题满分13分)
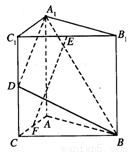 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求A1B与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B-A1D-A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
如图,直三棱柱![]() 中,AB=2,
中,AB=2,
![]() ,
,![]()
(Ⅰ)求直三棱柱![]() 侧视图的面积;
侧视图的面积;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在线段A1C上是否存在一点P,使PC1与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?如果存在,求出P点与C点的距离;如果不存在,请说明理由.
?如果存在,求出P点与C点的距离;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com