练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
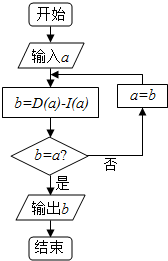
    19．已知集合A-{1，2，3，4，5，6，7，8，9），在集合A中任取三个元素，分别作为一个三位数的个位数，十位数和百位数，记这个三位数为a，现将组成a的三个数字按从小到大排成的三位数记为I（a），按从大到小排成的三位数记为D（a）（例如a=219，则I（a）=129，D（a）=921），阅读如图所示的程序框图，运行相应的程序，任意输入一个a，则输出b的值为（　　）
    A．792B．693C．594D．495

    分析 利用验证法判断求解即可．

    解答 解：A，如果输出b的值为792，则a=792，
    I（a）=279，D（a）=972，b=D（a）-I（a）=972-279=693，不满足题意．
    B，如果输出b的值为693，则a=693，
    I（a）=369，D（a）=963，b=D（a）-I（a）=963-369=594，不满足题意．
    C，如果输出b的值为594，则a=594，
    I（a）=459，D（a）=954，b=D（a）-I（a）=954-459=495，不满足题意．
    D，如果输出b的值为495，则a=495，
    I（a）=459，D（a）=954，b=D（a）-I（a）=954-459=495，满足题意．
    故选：D．

    点评 本题主要考查了循环结构的程序框图，用验证法求解是解题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．如图，已知PA为⊙O的切线，A为切点，直线PO交⊙O于点E、F，过点A作PO的垂线交⊙O于点B，垂足为D．
    证明：EF2=4OD•OP．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．若函数f（x）=ax3+2bx2-4x在x=-2与$x=\frac{2}{3}$处取得极值．
    （1）求函数f（x）的解析式；
    （2）求函数f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．正方体ABCD-A′B′C′D′棱长为1
    （1）证明：面A′BD∥面B′CD′
    （2）求点B′到面A′BD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知数列{an}，${a_n}∈{N^*}$，${S_n}=\frac{1}{8}{（{a_n}+2）^2}$，求an=4n-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知向量$\overrightarrow{a}$=（2cosx，1），向量$\overrightarrow{b}$=（cosx，$\sqrt{3}$sin 2x），设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，x∈R．
    （I）求函数f（x）的最小正周期；
    （Ⅱ）当x∈[$-\frac{π}{6}$，$\frac{π}{3}$]时，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

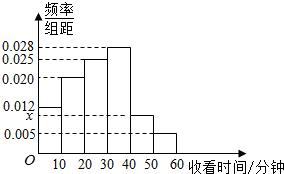    11．某电视传媒公司为了了解某类体育节目的收视情况，随机抽取了100名观众进行调查，如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图，其中收看时间分组区间是：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]．则图中x的值为0.01．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．等差数列{an}中，a2=5，a1+a5=12．
    （1）求数列{an}的通项公式；
    （2）设bn=2${\;}^{{a}_{n}-3}$+n，求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设集合A={x||x-a|＜1，x∈R}，B={y|y=lg（x2+1），x∈R}，若A⊆B，则实数a的取值范围是（　　）
    A．{a|a＞1}B．{a|a≥1}C．{a|a≥-1}D．{a|a＞-1}

    查看答案和解析>>

    同步练习册答案