
【题目】已知椭圆![]() ,且椭圆C上恰有三点在集合
,且椭圆C上恰有三点在集合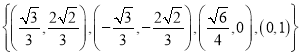 中.
中.
(1)求椭圆C的方程;
(2)若点O为坐标原点,直线AB与椭圆交于A、B两点,且满足![]() ,试探究:点O到直线AB的距离是否为定值.如果是,请求出定值:如果不是,请明说理由.
,试探究:点O到直线AB的距离是否为定值.如果是,请求出定值:如果不是,请明说理由.
(3)在(2)的条件下,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)点O到直线AB的距离为定值
(2)点O到直线AB的距离为定值![]() (3)
(3)![]()
【解析】
(1)利用椭圆的对称性得椭圆必过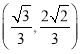 和
和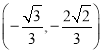 ,结合椭圆过点
,结合椭圆过点![]() ,求得
,求得![]() 的值,从而得到椭圆的方程;
的值,从而得到椭圆的方程;
(2)设![]() ,
,![]() ,对直线的斜率进行讨论,当斜率存在时设为
,对直线的斜率进行讨论,当斜率存在时设为![]() ,
,
由![]() 得
得![]() ,代入点到直线的距离公式可得答案;
,代入点到直线的距离公式可得答案;
(3)将弦![]() 表示成关于
表示成关于![]() 的函数,利用基本不等式求得弦
的函数,利用基本不等式求得弦![]() 的最大值,再代入三角形的面积公式,求得三角形面积的最大值.
的最大值,再代入三角形的面积公式,求得三角形面积的最大值.
(1)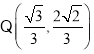 和
和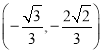 关于原点对称,故由题意知,椭圆C必过此两点
关于原点对称,故由题意知,椭圆C必过此两点
![]() ,又当椭圆过点
,又当椭圆过点![]() 时,
时,![]() ,∴
,∴![]() ,
,
此时满足![]() ,符合题意.
,符合题意.
所以椭圆![]() .
.
又当椭圆过点 时,
时,![]() ,∴
,∴![]() ,
,
此时![]() ,不符合题意.
,不符合题意.
综上:椭圆![]() .
.
(2)设![]() ,
,![]() ,若斜率存在,则设直线
,若斜率存在,则设直线![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
,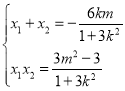
由![]() 知,
知,
![]() ,
,
代入得![]() ,
,
又原点到直线AB的距离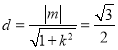 ,
,
且当AB的斜率不存在时,![]() ,可得
,可得![]() ,依然成立.
,依然成立.
所以点O到直线AB的距离为定值![]() .
.
(3)由(2)知,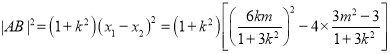
由(2)知,![]() ,
,
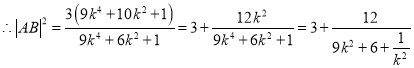 ;
;
因为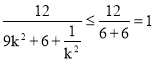 ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
所以![]() ;
;
易知当AB斜率不存在时,![]() ,所以
,所以![]() ,
,
综上得![]() 的面积的最大值为
的面积的最大值为![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,
,![]() ,
,![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)若![]() .①当
.①当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
②证明![]() 是定值,并求出此定值.
是定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的.在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样,对于直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样,对于直角坐标系内任意两点![]() 、
、![]() 定义它们之间的一种“距离”(“直角距离”):
定义它们之间的一种“距离”(“直角距离”):![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() (
(![]() ,
,![]() )上一点
)上一点![]() 到原点
到原点![]() 的“距离”;
的“距离”;
(2)求所有到定点![]() 的“距离”均为2的动点围成的图形的周长;
的“距离”均为2的动点围成的图形的周长;
(3)在“欧式几何学”中有如下三个与“距离”有关的正确结论:
①平面上任意三点A,B,C,![]() ;
;
②平面上不在一直线上任意三点A,B,C,若![]() ,则
,则![]() 是以
是以![]() 为直角三角形
为直角三角形
③平面上存在两个不同的定点A,B,若动点P满足![]() ,则动点P的轨迹是
,则动点P的轨迹是![]() 的垂直平分线
的垂直平分线
上述结论对于“出租车几何学”中的直角距离是否还正确,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
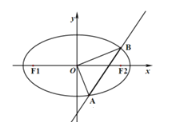
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,∠DAB=60°.
(1)求证:直线AM∥平面PNC;
(2)求二面角D﹣PC﹣N的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com