
分析 (1)化简g(x)=$\frac{lnx}{x+1}$+$\frac{a}{2x}$+$\sqrt{x}$,从而求导g′(x)=$\frac{\frac{1}{x}(x+1)-lnx}{(x+1)^{2}}$-$\frac{a}{2{x}^{2}}$+$\frac{1}{2\sqrt{x}}$,从而令g′(1)=$\frac{1}{2}$-$\frac{a}{2}$+$\frac{1}{2}$=0即可解得;
(2)化简可得$\frac{lnx}{x+1}$+$\frac{1}{x}$>$\frac{n}{x}$,从而可得n<$\frac{xlnx}{x+1}+1$=$\frac{xlnx+x+1}{x+1}$,可判断$\frac{xlnx}{x+1}+1$>0且$\frac{1ln1}{1+1}$+1=1,从而求得.
解答 解:(1)∵f(x)=$\frac{lnx}{x+1}$+$\frac{a}{2x}$,
∴g(x)=$\frac{lnx}{x+1}$+$\frac{a}{2x}$+$\sqrt{x}$,
∴g′(x)=$\frac{\frac{1}{x}(x+1)-lnx}{(x+1)^{2}}$-$\frac{a}{2{x}^{2}}$+$\frac{1}{2\sqrt{x}}$,
∵x=1是函数g(x)的极值点,
∴g′(1)=$\frac{1}{2}$-$\frac{a}{2}$+$\frac{1}{2}$=0,
解得,a=2;
经检验,g(x)在x=1处有极小值;
(2)由(1)知,f(x)=$\frac{lnx}{x+1}$+$\frac{1}{x}$,又∵f(x)>$\frac{n}{x}$,
∴$\frac{lnx}{x+1}$+$\frac{1}{x}$>$\frac{n}{x}$,
即n<$\frac{xlnx}{x+1}+1$=$\frac{xlnx+x+1}{x+1}$,
令m(x)=xlnx+x+1,
则m′(x)=lnx+1+1,
故m(x)在(0,e-2)上是减函数,在(e-2,+∞)上是增函数,
故m(x)>m(e-2)=1-e-2>0,
故$\frac{xlnx}{x+1}+1$>0恒成立;
又∵$\frac{1•ln1}{1+1}$+1=1,
∴n<1;
故整数n的最大值为0.
点评 本题考查了导数的综合应用,同时考查了恒成立问题,关键在于判断$\frac{xlnx}{x+1}+1$>0且$\frac{1ln1}{1+1}$+1=1.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
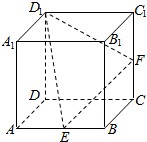 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | BC∥平面PDF | B. | DF⊥平面PAE | C. | 平面PDE⊥平面ABC | D. | 平面PDF⊥平面PAE |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<1} | B. | {x|0≤x≤1} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com