[题目]某公司为改善职工的出行条件.随机抽取50名职工.调查他们的居住地与公司的距离d．若样本数据分组为[0.2].(2.4].(4.6].(6.8].(8.10].(10.12].由数据绘制的分布频率直方图如图所示.则样本中职工居住地与公司的距离不超过4千米的人数为人．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某公司为改善职工的出行条件，随机抽取50名职工，调查他们的居住地与公司的距离d（单位：千米）．若样本数据分组为[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]，由数据绘制的分布频率直方图如图所示，则样本中职工居住地与公司的距离不超过4千米的人数为人．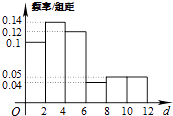

【答案】24
【解析】解：样本中职工居住地与公司的距离不超过4千米的频率为：（0.1+0.14）×2=0.48，所以样本中职工居住地与公司的距离不超过4千米的人数为：50×0.48=24人
所以答案是：24．
【考点精析】利用频率分布直方图对题目进行判断即可得到答案，需要熟知频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（吨）与相应的生产能耗（吨）标准煤的几组对照数据：

	3	4	5	6
	2.5	3	4	4.5

（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

（2）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？

（参考：）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若函数y=f（x）图象上存在不同的两点A，B关于y轴对称，则称点对[A，B]是函数y=f（x）的一对“黄金点对”（注：点对[A，B]与[B，A]可看作同一对“黄金点对”）．已知函数f（x）=，则此函数的“黄金点对“有（　　）

A. 0对B. 1对C. 2对D. 3对

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（1）若数列的前n项和，求数列的通项公式.

（2）若数列的前n项和，证明为等比数列.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设a，b，c，d均为正数，且a+b=c+d，证明：
（1）若ab＞cd，则 + ＞ + ；
（2） + ＞ + 是|a﹣b|＜|c﹣d|的充要条件．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划.年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本万元，每生产（百辆），需另投入成本万元，且.由市场调研知，每辆车售价万元，且全年内生产的车辆当年能全部销售完.