
【题目】若![]() 、
、![]() 是函数
是函数![]() (
(![]() ,
,![]() )的两个不同的零点,且
)的两个不同的零点,且![]() 、
、![]() 、
、![]() 适当排序后可构成等差数列,也可适当排序后构成等比数列,则
适当排序后可构成等差数列,也可适当排序后构成等比数列,则![]() ________
________
【答案】![]()
【解析】
a,b是函数f(x)=x2px+q(p>0,q>0)的两个不同的零点,可得a+b=p,ab=q,p>0,q>0,△=p24q>0.不妨设a<b.由于a,b,4这三个数可适当排序后成等差数列,也可适当排序后成等比数列,可得4,a,b或b,a,4成等差数列,a,4,b或b,4,a成等比数列,即可得出.
解:∵a,b是函数f(x)=x2px+q(p>0,q>0)的两个不同的零点,
∴a+b=p,ab=q,p>0,q>0,△=p24q>0.
不妨设a<b.
由于a,b,4这三个数可适当排序后成等差数列,也可适当排序后成等比数列,
∴4,a,b或b,a,4成等差数列,a,4,b或b,4,a成等比数列,
∴b4=2a,ab=(4)2,
解得a=2,b=8.
∴p=10,q=16.
满足△≥0.
则p+q=26.
故选:C.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
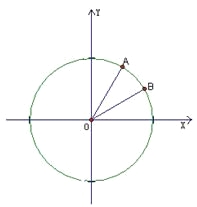
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律.现把杨辉三角中的数从上到下,从左到右依次排列,得数列:![]() .记作数列
.记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ___ .
___ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上在第二象限内的一点,且直线
上在第二象限内的一点,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 点的坐标;
点的坐标;
(2)过点![]() 作一条斜率为正数的直线
作一条斜率为正数的直线![]() 与椭圆
与椭圆![]() 从左向右依次交于
从左向右依次交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 是增函数,其图像如图所示.
是增函数,其图像如图所示.

(1)已知![]() ,
,![]() ,利用上述性质,求函数
,利用上述性质,求函数![]() 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A.顺序结构是由若干个依次执行的步骤组成的,每一个算法都离不开顺序结构
B.循环结构是在一些算法中从某处开始,按照一定的条件,反复执行某些步骤,所以循环结构中一定包含条件结构
C.循环结构中不一定包含条件结构
D.用程序框图表示算法,使之更加直观形象,容易理解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人用农药治虫,由于计算错误,在A,B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个能容纳1千克药水的药瓶,他们从A,B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为an%,B喷雾器中药水的浓度为bn%.
(1)证明an+bn是一个常数;
(2)求an与an-1的关系式;
(3)求an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() ,过直线
,过直线![]() :
:![]() 上任一点
上任一点![]() 向抛物线
向抛物线![]() 引两条切线
引两条切线![]() (切点为
(切点为![]() ,且点
,且点![]() 在
在![]() 轴上方).
轴上方).
(1)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com