
【题目】如图,在四棱锥![]() 中,底而
中,底而![]() 为菱形,且菱形
为菱形,且菱形![]() 所在的平面与
所在的平面与![]() 所在的平面相互垂直,
所在的平面相互垂直,![]() ,
,![]() ,
,![]() ,
,![]() .
.
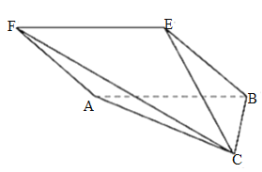
(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的最长侧棱的长.
的最长侧棱的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在菱形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由此可证.
,由此可证.
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,由已知易得:
,由已知易得:![]() 是正三角形,
是正三角形,![]() ,进一步可证
,进一步可证![]() 平面
平面![]() ,由勾股定理可求出侧棱
,由勾股定理可求出侧棱![]() ,
,![]() ,
,![]() ,
,![]() 的长度,得到最长的是
的长度,得到最长的是![]() ,或可先判断CF最长,求解出长度即可.
,或可先判断CF最长,求解出长度即可.
(1)在菱形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
(2)方法一:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知易得:![]() 是正三角形,∴
是正三角形,∴![]() .
.
又∴平面![]() 平面
平面![]() 且交线为
且交线为![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,
,
在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
显然在侧棱![]() ,
,![]() ,
,![]() ,
,![]() 中最长的是
中最长的是![]() .
.
∴四棱锥![]() 的最长侧棱的长为
的最长侧棱的长为![]() .
.
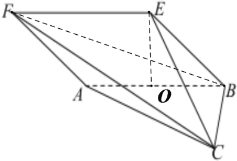
方法二:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知易得:![]() 是正三角形,∴
是正三角形,∴![]() ,
,
又∵平面![]() 平面
平面![]() 且交线为
且交线为![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ∴
∴![]() ,
,![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() 最长.
最长.
在![]() 中,
中,![]() .
.
∴四棱锥![]() 的最长侧棱的长为
的最长侧棱的长为![]() .
.


科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某高校综合评价有两步:第一步是材料初审,若材料初审不合格,则不能进入第二步面试;若材料初审合格,则进入第二步面试.只有面试合格者,才能获得该高校综合评价的录取资格,现有A,B,C三名学生报名参加该高校的综合评价,假设A,B,C三位学生材料初审合格的概率分别是![]() ,
,![]() ,
,![]() ;面试合格的概率分别是
;面试合格的概率分别是![]() ,
,![]() ,
,![]() .
.
(1)求A,B两位考生有且只有一位考生获得录取资格的概率;
(2)记随机变量X为A,B,C三位学生获得该高校综合评价录取资格的人数,求X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了了解业主用水情况,该小区分为一期和二期,入住共达4000户,现在通过随机抽样获得了100户居民的月均用水量,下图是调查结果的频数分布表和频率分布直方图.
分组 |
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 |
分组 |
|
|
|
| |
频数 | 14 | 6 | 4 | 2 |
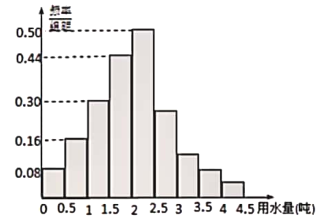
(1)估计该小区月均用水量超过3.8吨约有多少户;(2)通过频率分布直方图,估计该小区居民月均用水量平均值和中位数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场春节期间推出一项优惠活动,活动规则如下:消费额每满300元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在区域Ⅰ返券60元;停在区域Ⅱ返券30元;停在区域Ⅲ不返券.例如:消费600元,可抽奖2次,所获得的返券金额是两次金额之和.
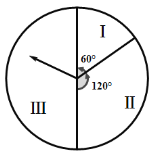
(Ⅰ)若某位顾客消费300元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费600元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,根据船
的左支上,根据船![]() 接收到
接收到![]() 台和
台和![]() 台电磁波的时间差,计算出船
台电磁波的时间差,计算出船![]() 到
到![]() 发射台的距离比到
发射台的距离比到![]() 发射台的距离远30海里,则点
发射台的距离远30海里,则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )

A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com