
 、
、 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R). 、
、 起点相同,t为何值时,若
起点相同,t为何值时,若 、t
、t 、
、 (
( +
+ )三向量的终点在一直线上?
)三向量的终点在一直线上? |=|
|=| |且
|且 与
与 是夹角为60°,那么t为何值时,|
是夹角为60°,那么t为何值时,| -t
-t |有最小?
|有最小?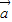 -t
-t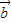 =m[
=m[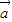 -
- (
(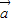 +
+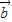 )](m∈R),
)](m∈R),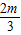 -1)
-1)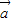 =(
=(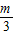 -t)
-t)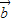 .
.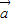 与
与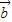 不共线,
不共线,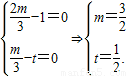
 时,
时,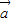 、t
、t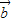 、
、 (
(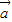 +
+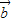 )的终点在一直线上.
)的终点在一直线上.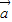 -t
-t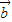 |2=(
|2=(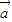 -t
-t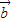 )2=|
)2=|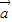 |2+t2|
|2+t2|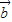 |2-2t|
|2-2t|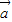 ||
||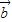 |cos60°=(1+t2-t)|
|cos60°=(1+t2-t)|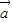 |2,
|2, 时,|
时,|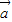 -t
-t |有最小值
|有最小值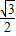 |
|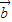 |.
|.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2010-2011学年广东省广州113中学高一(下)期中数学试卷(解析版) 题型:解答题
 、
、 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R). 、
、 起点相同,t为何值时,若
起点相同,t为何值时,若 、t
、t 、
、 (
( +
+ )三向量的终点在一直线上?
)三向量的终点在一直线上? |=|
|=| |且
|且 与
与 是夹角为60°,那么t为何值时,|
是夹角为60°,那么t为何值时,| -t
-t |有最小?
|有最小?查看答案和解析>>
科目:高中数学 来源:《平面向量》2013年山东省高考数学一轮复习单元测试(理科)(解析版) 题型:解答题
 、
、 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R). 、
、 起点相同,t为何值时,若
起点相同,t为何值时,若 、t
、t 、
、 (
( +
+ )三向量的终点在一直线上?
)三向量的终点在一直线上? |=|
|=| |且
|且 与
与 是夹角为60°,那么t为何值时,|
是夹角为60°,那么t为何值时,| -t
-t |有最小?
|有最小?查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省天门市岳口高中高考专项复习:向量(文科)(解析版) 题型:解答题
 、
、 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R). 、
、 起点相同,t为何值时,若
起点相同,t为何值时,若 、t
、t 、
、 (
( +
+ )三向量的终点在一直线上?
)三向量的终点在一直线上? |=|
|=| |且
|且 与
与 是夹角为60°,那么t为何值时,|
是夹角为60°,那么t为何值时,| -t
-t |有最小?
|有最小?查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:5.1 向量的概念、向量的加法与减法、实数与向量的积(解析版) 题型:解答题
 、
、 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R). 、
、 起点相同,t为何值时,若
起点相同,t为何值时,若 、t
、t 、
、 (
( +
+ )三向量的终点在一直线上?
)三向量的终点在一直线上? |=|
|=| |且
|且 与
与 是夹角为60°,那么t为何值时,|
是夹角为60°,那么t为何值时,| -t
-t |有最小?
|有最小?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com