分析:方程x3-3x-m=0有且只有两个不同的实根等价于函数f(x)=x3-3x和y=m有且只有两个不同的交点,由导数工具可画出函数的图象,数形结合可得答案.
解答: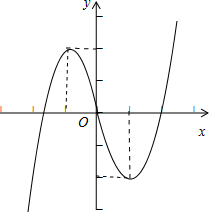
解:方程x
3-3x-m=0有且只有两个不同的实根等价于
函数f(x)=x
3-3x和y=m有且只有两个不同的交点,
而f′(x)=3x
2-3,令3x
2-3=0可得x=±1,
当x∈(-∞,-1)时,f′(x)=3x
2-3>0,函数f(x)=x
3-3x单调递增,
当x∈(-1,1)时,f′(x)=3x
2-3<0,函数f(x)=x
3-3x单调递减,
当x∈(1,+∞)时,f′(x)=3x
2-3>0,函数f(x)=x
3-3x单调递增,
故函数f(x)=x
3-3x在x=-1处取到极大值f(-1)=2,在x=1处取到极小值f(1)=-2,
故其图象如图所示:
可知m=±2
故答案为:±2
点评:本题考查三次方程的根的个数问题,转化为函数图象交点个数是解决问题的关键,属中档题.

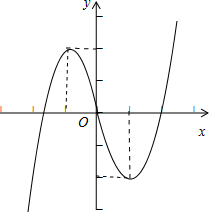 解:方程x3-3x-m=0有且只有两个不同的实根等价于
解:方程x3-3x-m=0有且只有两个不同的实根等价于
