

| A. | $-\frac{1}{3}$ | B. | $-\frac{1}{6}$ | C. | 0 | D. | $\frac{1}{3}$ |
分析 由函数图象得$f(x)=\left\{\begin{array}{l}{-x-1,-1≤x≤0}\\{x-1,0<x≤1}\end{array}\right.$,由此能求出$\int_{-1}^1{[xf(x)]}dx$的值.
解答 解:∵函数y=f(x)的图象为如图所示的折线ABC,
∴$f(x)=\left\{\begin{array}{l}{-x-1,-1≤x≤0}\\{x-1,0<x≤1}\end{array}\right.$,
∴$\int_{-1}^1{[xf(x)]}dx$=${∫}_{-1}^{0}(-x-1)dx+{∫}_{0}^{1}(x-1)dx$
=(-$\frac{1}{2}{x}^{2}$-x)${|}_{-1}^{0}$+($\frac{1}{2}{x}^{2}-x$)${|}_{0}^{1}$
=(-$\frac{1}{2}+1$)+($\frac{1}{2}-1$)
=0.
故选:C.
点评 本题考查函数的定积分的求法,是基础题,解题时要认真审题,注意定积分的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
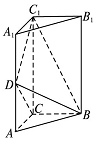 如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,$CA=CB=\frac{1}{2}C{C_1}$,点D棱AA1的中点,且C1D⊥BD.
如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,$CA=CB=\frac{1}{2}C{C_1}$,点D棱AA1的中点,且C1D⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空间四边形 | B. | 任意的四边形 | C. | 梯形 | D. | 平行四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{3}$ | B. | $±\sqrt{13}$ | C. | ±4 | D. | $±2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,2) | C. | $[{1,\frac{3}{2}})$ | D. | $({1,\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
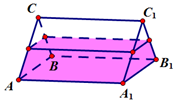 如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )
如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )| A. | 7 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com