
 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个? ,且an>0. td 当n=1时,4
,且an>0. td 当n=1时,4 +2a1,解得a1=2.当n≥2时,有4Sn-1=
+2a1,解得a1=2.当n≥2时,有4Sn-1= .于是4
.于是4 .故(an+an-1)(an-an-1)=2(an+an-1).由此能证明数列{an}是首项为2,公差为2的等差数列,且an=2n.
.故(an+an-1)(an-an-1)=2(an+an-1).由此能证明数列{an}是首项为2,公差为2的等差数列,且an=2n. ,由此能够证明
,由此能够证明 +
+ +…+
+…+ <1.
<1.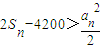 ,得2n(n+1)-4200>2n2,所以n>2100.故M={2000,2002,…,2008,2010,2012,…,2998}.由此能够求出集合M中满足条件的正整数m的个数.
,得2n(n+1)-4200>2n2,所以n>2100.故M={2000,2002,…,2008,2010,2012,…,2998}.由此能够求出集合M中满足条件的正整数m的个数. ,且an>0. …(1分)
,且an>0. …(1分) +2a1,解得a1=2. …(2分)
+2a1,解得a1=2. …(2分) .
. ,
, .
. ,
, ,…(5分)
,…(5分)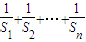 =(1-
=(1- )+(
)+( )+…+(
)+…+( )
)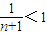 .…(7分)
.…(7分)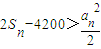 ,
, +
+ +…+
+…+ <1和求集合中元素的个数.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意裂项求和法的合理运用.
<1和求集合中元素的个数.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意裂项求和法的合理运用. 

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| an+1 |
| an |
| an |
| an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2a2m(1+S2n) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com