
【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力。某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果。例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
视觉 听觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 | b | |
偏高 | 2 | a | 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() 。
。
(1)试确定a,b的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为X,求随机变量X的分布列。
【答案】(1)a=6,b=2;(2)见解析
【解析】
(1)由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人.记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,事件A的概率即为![]() ,由此建立方程即可求出a,b;
,由此建立方程即可求出a,b;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为ξ,ξ的可能取值为0,1,2,3,分别求出其概率列出分布列.
(1)由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人。记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,
则P(A)=![]() ,解得a=6,从而b=40-(32+a)=40-38=2。
,解得a=6,从而b=40-(32+a)=40-38=2。
(2)由于从40位学生中任意抽取3位的结果数为![]() ,
,
其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,
从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为![]() ,
,
所以从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的概率为P(X=k)=![]() (k=0,1,2,3)。X的可能取值为0,1,2,3。
(k=0,1,2,3)。X的可能取值为0,1,2,3。
因为P(X=0)=![]() ,P(X=1)=
,P(X=1)=![]() ,
,
P(X=2)=![]() ,P(X=3)=
,P(X=3)=![]() ,
,
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】如图,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
折起到![]() 的位置,使
的位置,使![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求三棱柱
)求三棱柱![]() 的体积.
的体积.
(![]() )线段
)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() .若存在,指出点
.若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探究与发现:为什么二次函数![]() 的图象是抛物线?我们知道,平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线,这是抛物线的定义,也是其本质特征
的图象是抛物线?我们知道,平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线,这是抛物线的定义,也是其本质特征![]() 因此,只要说明二次函数的图象符合抛物线的本质特征,就解决了为什么二次函数
因此,只要说明二次函数的图象符合抛物线的本质特征,就解决了为什么二次函数![]() 的图象是抛物线的问题
的图象是抛物线的问题![]() 进一步讲,由抛物线与其方程之间的关系可知,如果能用适当的方式将
进一步讲,由抛物线与其方程之间的关系可知,如果能用适当的方式将![]() 转化为抛物线标准方程的形式,那么就可以判定二次函数
转化为抛物线标准方程的形式,那么就可以判定二次函数![]() 的图象是抛物线了.下面我们就按照这个思路来展开.对二次函数式
的图象是抛物线了.下面我们就按照这个思路来展开.对二次函数式![]() 的右边配方,得
的右边配方,得![]() .由函数图象平移
.由函数图象平移![]() 一般地,设
一般地,设![]() 是坐标平面内的一个图形,将
是坐标平面内的一个图形,将![]() 上所有点按照同一方向,移动同样的长度,得到图形
上所有点按照同一方向,移动同样的长度,得到图形![]() ,这一过程叫作图形的平移
,这一过程叫作图形的平移![]() 的知识可以知道,沿向量
的知识可以知道,沿向量![]() 平移函数
平移函数![]() 的图象
的图象![]() 如图,函数图象的形状、大小不发生任何变化,平移后图象对应的函数解析式为
如图,函数图象的形状、大小不发生任何变化,平移后图象对应的函数解析式为![]() ,我们把它改写为
,我们把它改写为![]() 的形式
的形式![]() 方程
方程![]() ,这是顶点为坐标原点,焦点为
,这是顶点为坐标原点,焦点为![]() 的抛物线.这样就说明了二次函数
的抛物线.这样就说明了二次函数![]() 的图象是一条抛物线.
的图象是一条抛物线.
请根据以上阅读材料,回答下列问题:
![]() 由函数
由函数![]() 的图象沿向量
的图象沿向量![]() 平移,得到的图象对应的函数解析式为
平移,得到的图象对应的函数解析式为![]() ,求
,求![]() 的坐标;
的坐标;
![]() 过抛物线
过抛物线![]() 的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q,试探究
的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q,试探究![]() 是否为定值?并说明理由.
是否为定值?并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同
![]() 从盒子中随机取出2个球,求取出的2个球颜色相同的概率.
从盒子中随机取出2个球,求取出的2个球颜色相同的概率.
![]() 从盒子中随机取出4个球,其中红球个数分别记为X,求随机变量X的分布列和数学期望.
从盒子中随机取出4个球,其中红球个数分别记为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=![]() ,EF=1,BC=
,EF=1,BC=![]() ,且M是BD的中点。
,且M是BD的中点。

(1)求证:EM∥平面ADF;
(2)求二面角D-AF-B的余弦值;
(3)在线段ED上是否存在一点P,使得BP∥平面ADF?若存在,求出EP的长度;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
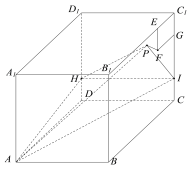
【题目】如图所示,正方体ABCD﹣A1B1C1D1棱长为4,点![]() 在棱
在棱![]() 上,点
上,点![]() 在棱
在棱![]() 上,且
上,且![]() .在侧面
.在侧面![]() 内以
内以![]() 为一个顶点作边长为1的正方形
为一个顶点作边长为1的正方形![]() ,侧面
,侧面![]() 内动点
内动点![]() 满足到平面
满足到平面![]() 距离等于线段
距离等于线段![]() 长的
长的![]() 倍,则当点
倍,则当点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积的最小值是( )
的体积的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的两个函数
上的两个函数![]() 和
和![]() ,如果对任意的
,如果对任意的![]() ,均有不等式
,均有不等式![]() 成立,则称函数
成立,则称函数![]() 与
与![]() 在
在![]() 上是“友好”的,否则称为“不友好”的.
上是“友好”的,否则称为“不友好”的.
(1)若![]() ,
,![]() ,则
,则![]() 与
与![]() 在区间
在区间![]() 上是否“友好”;
上是否“友好”;
(2)现在有两个函数![]() 与
与![]() ,给定区间
,给定区间![]() .
.
①若![]() 与
与![]() 在区间
在区间![]() 上都有意义,求
上都有意义,求![]() 的取值范围;
的取值范围;
②讨论函数![]() 与
与![]() 与在区间
与在区间![]() 上是否“友好”.
上是否“友好”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com