
分析 (1)分别求得f(x),g(x)的导数,求得切线的斜率,解方程可得t=1,即可得到切线的斜率和切点坐标,可得切线的方程;
(2)设函数h(x)=f(x)-g(x),“曲线y=f(x)与y=g(x)有且仅有一个公共点”等价于“函数y=h(x)有且仅有一个零点”.对h(x)求导,讨论①当t≤0时,②当t=1时,③当0<t<1时,求出单调区间,即可得到零点和所求范围
解答 解:(1)求导,得f′(x)=2x,g′(x)=$\frac{2t}{x}$,(x>0).
由题意,得切线l的斜率k=f′(1)=g′(1),
即k=2t=2,解得t=1.
又切点坐标为(1,0),
所以切线l的方程为2x-y-2=0;
(2)设函数h(x)=f(x)-g(x)=x2-1-2tlnx,x∈(0,+∞).
“曲线y=f(x)与y=g(x)有且仅有一个公共点”等价于
“函数y=h(x)有且仅有一个零点”.
求导,得h′(x)=2x-$\frac{2t}{x}$.
①当t≤0时,由x∈(0,+∞),得h'(x)>0,
所以h(x)在(0,+∞)单调递增.
又因为h(1)=0,所以y=h(x)有且仅有一个零点1,符合题意.
②当t=1时,当x变化时,h'(x)与h(x)的变化情况如下表所示:
| x | (0,1) | 1 | (1,+∞) |
| h'(x) | - | 0 | + |
| h(x) | ↘ | 极小值 | ↗ |
| x | (0,$\sqrt{t}$) | $\sqrt{t}$ | ($\sqrt{t}$,+∞) |
| h'(x) | - | 0 | + |
| h(x) | ↘ | 极小值 | ↗ |
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查函数的零点问题的解法,注意运用构造法,通过导数求得单调性,同时考查分类讨论的思想方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{39}}}{39}$ | B. | $\frac{{\sqrt{13}}}{13}$ | C. | $\frac{{\sqrt{13}}}{39}$ | D. | $\frac{{\sqrt{39}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 [普通中学做]如图所示,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点Q的横坐标为$\frac{4}{5}$.
[普通中学做]如图所示,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点Q的横坐标为$\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出多项式求值的秦九韶算法,如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,依次输入a为2,2,5,则输出的s=( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出多项式求值的秦九韶算法,如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,依次输入a为2,2,5,则输出的s=( )| A. | 7 | B. | 12 | C. | 17 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{10}{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
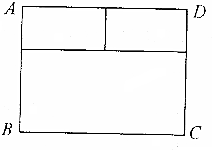 有根木料长6米,要做一个如图的窗框,已知上框架与下框架的高比为1:2,问怎样利用木料,才能使光线通过窗框面积最大?并求出最大面积.(中间木挡的面积可忽略不计)
有根木料长6米,要做一个如图的窗框,已知上框架与下框架的高比为1:2,问怎样利用木料,才能使光线通过窗框面积最大?并求出最大面积.(中间木挡的面积可忽略不计)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1,4) | B. | (-2,1,-4) | C. | (2,1,-4) | D. | (2,-1,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com