
分析 根据已知将分母进行拆分,根据裂项法,求出m,n的值,代入足C${\;}_{t}^{m}$=C${\;}_{t}^{n}$,根据排列组合的性质可求得t的值.
解答 解:1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{m}$+$\frac{1}{20}$+$\frac{1}{n}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$,
∵2=1×2,
6=2×3,
30=5×6,
42=6×7,
56=7×8,
72=8×9,
90=9×10,
110=10×11,
132=11×12,
1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{m}$+$\frac{1}{20}$+$\frac{1}{n}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$=(1-$\frac{1}{4}$)+$\frac{1}{m}$+$\frac{1}{20}$+$\frac{1}{n}$+($\frac{1}{6}$-$\frac{1}{12}$)+$\frac{1}{156}$,
$\frac{1}{m}$+$\frac{1}{n}$=$\frac{m+n}{mn}$=$\frac{43}{390}$,
中m,n∈N*,且m<n,
解得m=13,n=30,
C${\;}_{t}^{m}$=C${\;}_{t}^{n}$,
∴m+n=t,
∴t=43,
故答案为:43.
点评 本题考查的知识点是归纳推理,排列组合的运算性质,其中根据已知求出m,n值是解答的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
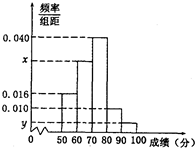 学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.
学校达标运动会后,为了解学生的体质情况,从中抽取了部分学生的成绩,得到一个容量为n的样本,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了如图的频率分布直方图,已知[50,60)与[90,100]两组的频数分别为24与6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
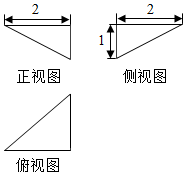
| A. | 2$\sqrt{2}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
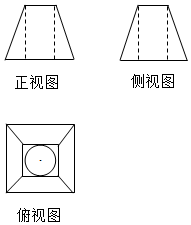 已知一个几何体的三视图如图所示,正视图和侧视图是两个的全等的等腰梯形,梯形上底、下底分别为2,4,腰长为$\sqrt{10}$,则该几何体的体积为( )
已知一个几何体的三视图如图所示,正视图和侧视图是两个的全等的等腰梯形,梯形上底、下底分别为2,4,腰长为$\sqrt{10}$,则该几何体的体积为( )| A. | $\frac{28}{3}$$\sqrt{10}$-3π | B. | 28-2π | C. | 28-3π | D. | $\frac{28}{3}$$\sqrt{10}$-2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
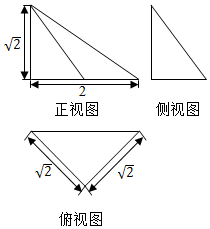
| A. | 2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{1000}$ | B. | $\frac{1}{1003}$ | C. | $\frac{50}{1000}$ | D. | $\frac{50}{1003}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com