
【题目】在四棱锥![]() 中,侧面PAD是等边三角形,且平面
中,侧面PAD是等边三角形,且平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
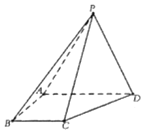
(1)AD上是否存在一点M,使得平面![]() 平面ABCD;若存在,请证明,若不存在,请说明理由;
平面ABCD;若存在,请证明,若不存在,请说明理由;
(2)若![]() 的面积为
的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,有一种赛车跑道类似“梨形”曲线,由圆弧![]() 和线段AB,CD四部分组成,在极坐标系Ox中,A(2,
和线段AB,CD四部分组成,在极坐标系Ox中,A(2,![]() ),B(1,
),B(1,![]() ),C(1,
),C(1,![]() ),D(2,
),D(2,![]() ),弧
),弧![]() 所在圆的圆心分别是(0,0),(2,0),曲线M1是弧
所在圆的圆心分别是(0,0),(2,0),曲线M1是弧![]() ,曲线M2是弧
,曲线M2是弧![]() .
.
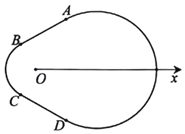
(1)分别写出M1,M2的极坐标方程:
(2)点E,F位于曲线M2上,且![]() ,求△EOF面积的取值范围.
,求△EOF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥底面ABCD,E在PB上.
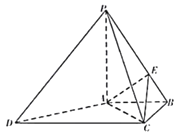
(1)证明:AC⊥PD;
(2)若PE=2BE,求三棱锥P﹣ACE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了60名男顾客和80名女顾客,每位顾客均对该商场的服务给出满意或不满意的评价,得到下面不完整的列联表:
满意 | 不满意 | 合计 | |
男顾客 | 50 | ||
女顾客 | 50 | ||
合计 |
(1)根据已知条件将列联表补充完整;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
附: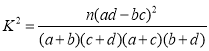
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面中,△ABC的两个顶点A、B的坐标分别为A(﹣1,0),B (1,0),平面内两点G、M同时满足下列条件:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ∥
∥![]() ,则△ABC的顶点C的轨迹方程为_____.
,则△ABC的顶点C的轨迹方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,过右焦点F的直线l与椭圆E交于A,B两点(A,B两点不在x轴上),椭圆E在A,B两点处的切线交于P,点P在定直线
,过右焦点F的直线l与椭圆E交于A,B两点(A,B两点不在x轴上),椭圆E在A,B两点处的切线交于P,点P在定直线![]() 上.
上.
(1)记点![]() ,求过点
,求过点![]() 与椭圆E相切的直线方程;
与椭圆E相切的直线方程;
(2)以![]() 为直径的圆过点F,求
为直径的圆过点F,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com