
【题目】已知函数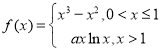 ,(
,(![]() ).
).
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设点![]() ,
,![]() 是函数
是函数![]() 图象的不同两点,其中
图象的不同两点,其中![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,且函数
,且函数![]() 在点
在点![]() 切线的斜率为
切线的斜率为![]() ,若存在,请求出
,若存在,请求出![]() 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
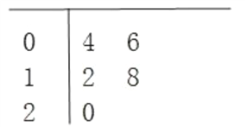
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.若
”表示乙村贫困户.若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;若
,则认定该户为“低收入户”;若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.

(1)从乙村的50户中随机选出一户,求该户为“绝对贫困户”的概率;
(2)从甲村所有“今年不能脱贫的非绝对贫困户”中任选2户,求选出的2户均为“低收入户”的概率;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=2,BC=1,F为线段CD上一动点(不含端点),现将△ADF沿直线AF进行翻折,在翻折过程中不可能成立的是( )

A.存在某个位置,使直线AF与BD垂直B.存在某个位置,使直线AD与BF垂直
C.存在某个位置,使直线CF与DA垂直D.存在某个位置,使直线AB与DF垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,点P(0,1).
,点P(0,1).
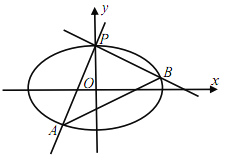
(1)过P点作斜率为k(k>0)的直线交椭圆C于A点,求弦长|PA|(用k表示);
(2)过点P作两条互相垂直的直线PA,PB,分别与椭圆交于A、B两点,试问:直线AB是否经过一定点?若存在,则求出定点,若不存在,则说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
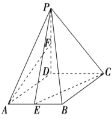
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集为
的解集为![]() ,且
,且![]() 在区间
在区间![]() 上的最小值是4.
上的最小值是4.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 在
在![]() 上的最大值
上的最大值![]() 、最小值
、最小值![]() 的解析式;
的解析式;
(3)设![]() ,若对任意
,若对任意![]() 均成立,求实数
均成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com