
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】每逢节日,电商之间的价格厮杀已经不是什么新鲜事,今年的6月18日也不例外.某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
顾客年龄 |
|
|
|
|
|
|
频数 | 4 | 24 | 32 | 20 | 16 | 4 |
(1)在下表中作出这些数据的频率分布直方图;
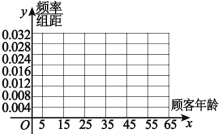
(2)用分层抽样的方法从这100名顾客中抽取25人,再从抽取的25人中随机抽取2人,求年龄在![]() 内的顾客人数
内的顾客人数![]() 的分布列、数学期望.
的分布列、数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
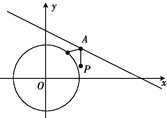
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马再回到军营,怎样走才能使总路程最短?在如图所示的直角坐标系xOy中,设军营所在平面区域为{(x,y)|x2+y2≤![]() },河岸线所在直线方程为x+2y-4=0.假定将军从点P(
},河岸线所在直线方程为x+2y-4=0.假定将军从点P(![]() ,
,![]() )处出发,只要到达军营所在区域即回到军营,当将军选择最短路程时,饮马点A的纵坐标为______.最短总路程为______
)处出发,只要到达军营所在区域即回到军营,当将军选择最短路程时,饮马点A的纵坐标为______.最短总路程为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程是![]() (t是参数).在以O为极点,x轴正半轴为极轴的极坐标系中,曲线
(t是参数).在以O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() .
.
(1)当![]() ,
,![]() 时,求直线l与曲线C的直角坐标方程;
时,求直线l与曲线C的直角坐标方程;
(2)当![]() 时,若直线l与曲线C相交于A,B两点,设
时,若直线l与曲线C相交于A,B两点,设![]() ,且
,且![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定圆![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程
的方程
(2)若轨迹![]() 上存在两个不同点
上存在两个不同点![]() ,
,![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情期间,为了减少外出聚集,“线上买菜”受追捧.某电商平台在![]() 地区随机抽取了
地区随机抽取了![]() 位居民进行调研,获得了他们每个人近七天“线上买菜”消费总金额(单位:元),整理得到如图所示频率分布直方图.
位居民进行调研,获得了他们每个人近七天“线上买菜”消费总金额(单位:元),整理得到如图所示频率分布直方图.
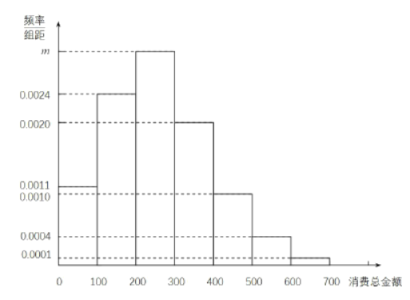
(1)求![]() 的值;
的值;
(2)从“线上买菜”消费总金额不低于![]() 元的被调研居民中,随机抽取
元的被调研居民中,随机抽取![]() 位给予奖品,求这
位给予奖品,求这![]() 位“线上买菜”消费总金额均低于
位“线上买菜”消费总金额均低于![]() 元的概率;
元的概率;
(3)若![]() 地区有
地区有![]() 万居民,该平台为了促进消费,拟对消费总金额不到平均水平一半的居民投放每人
万居民,该平台为了促进消费,拟对消费总金额不到平均水平一半的居民投放每人![]() 元的电子补贴.假设每组中的数据用该组区间的中点值代替,试根据上述频率分布直方图,估计该平台在
元的电子补贴.假设每组中的数据用该组区间的中点值代替,试根据上述频率分布直方图,估计该平台在![]() 地区拟投放的电子补贴总金额.
地区拟投放的电子补贴总金额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 相切于第二象限的点
相切于第二象限的点![]() ,与
,与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com