Question

【题目】已知数列{an}满足a1=﹣2，an+1=2an+4．
（1）证明数列{an+4}是等比数列并求出{an}通项公式；
（2）若 ，求数列{bn}的前n项和Sn ．

Answer 1

【答案】
（1）证明：∵a1=﹣2，∴a1+4=2，

∵an+1=2an+4，∴an+1+4=2an+8=2（an+4），

∴ ，

∴{an+4}是以2为首项，2为公比的等比数列，

由上知 ，∴ ．

（2）解：

∴ ，①

，②

②﹣①得：

=

=2+2n+1﹣2﹣（n+1）×2n+1

=﹣n2n+1．

【解析】（1）利用已知条件转化求解数列{an+4}是等比数列，然后求出{an}通项公式．（2）化简数列通项公式bn ， 利用错位相减法求和求解即可．
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系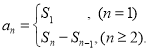；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．